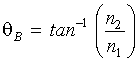Base geral da terminologia óptica
Anexo 3
Geometria das Telecentricas
Tabela de filtros Wratten
A temperatura e a natureza da cor
Polarização e célula de Kerr

Objetivas telecentricas.
Este seja talvez o tipo mais intrigante de objetivas especiais que diferem do sistema integrado de objetivas primárias propriamente dito. Este é o primeiro tipo que descreveremos. Os demais serão as objetivas de espelho e as zooms. Estas últimas estão no próximo anexo onde também descreveremos o funcionamento básico dos instrumentos ópticos e forneceremos um formulário geral de uso prático.
Que são objetivas telecentricas?
Atualmente se tem falado muito sobre objetivas telecentricas louvando-se em muito as suas qualidades sobre as objetivas convencionais. Na realidade são caras e de uso limitado. Suas características espetaculares de resolução dadas pelos fabricantes como extraordinariamente acima das ópticas convencionais são na realidade uma falácia pois os resultados por eles apresentados podem facilmente ser até superados por um simples menisco, se realizarmos os testes pelos padrões de onda monocromática coerente –isto é onda com exclusividade de um só comprimento- sem qualquer existência de bandas laterais ou presença de alguma outra cor que pudesse causar qualquer interferência. Portanto queremos aqui apresentar a verdade sobre os fatos e demonstrar o que vem ser a objetiva telecentrica.
Em primeiro lugar, poderemos definir como telecentrica qualquer óptica que tenha uma ou as duas pupilas de saída no infinito teórico. Isto é, um arranjo óptico tal como: um microscópio, um telescópio, uma luneta ou um binóculo terão em suas oculares raios emergentes paralelos, portanto serão também sistemas ópticos telecentricos na aceitação do termo. As objetivas telecentricas, contudo são utilizadas basicamente para manter no meio lente objeto (objeto-espaço) ou lente sensor (imagem-espaço) ou em ambos, raios paralelos com o intuito de medir corretamente objetos espaciais. Vamos elucidar na figura1, a seguir esta nossa definição. Na verdade o sistema telecentrico é um arranjo particularíssimo do sistema óptico que satisfaz condições excepcionais.
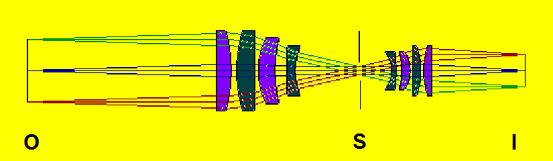
Fig 1:
Objetiva dupla telecentrica;
O sentido S - O vem a ser o sentido “objeto-espaço”.
O sentido I – S vem a ser o sentido “imagem espaço”.
Note que os vetores, são sempre orientados para a esquerda.
- As objetivas do tipo “objeto-espaço”, são normalmente usadas para a visão tipo máquina, com o intuito de manter invariáveis a geometria e dimensões do objeto visualizado independentemente das distâncias entre o observador e o objeto.
Uma objetiva do tipo imagem-espaço produz imagens do mesmo tamanho, independentemente das distâncias entre a lente e o filme (sensor). A focalização não altera as dimensões da imagem.
Objetivas telecentricas do tipo objeto-espaço geram imagens de objetos sempre do mesmo tamanho e possuem ângulos de visão constantes para todo o campo de visão. Mesmo que a imagem esteja fora de foco, esta terá as mesmas dimensões dela mesma quando em foco. São usadas em metrologia e litografia óptica para formar as placas de circuitos integrados.
- As objetivas do tipo “imagem-espaço”, são normalmente usadas com sensores de imagem que não toleram variação dos ângulos de incidência dos raios luminosos, como é o caso dos divisores de cor para os 3 CCD em câmaras de televisão. Nestes casos a interferência de cores e sombras é praticamente imperceptível.
- O terceiro tipo é usado para ampliações ou reduções fixas da imagem ou do objeto. Neste caso será chamada de uma dupla telecentrica isto é, quando estas propriedades de paralelismo forem mantidas para ambas posições.
Tecnicamente são apenas caracterizadas por sua ampliação ou redução em relação a imagem e objeto. Existem objetivas de ampliação fixas e variáveis tipo zoom,
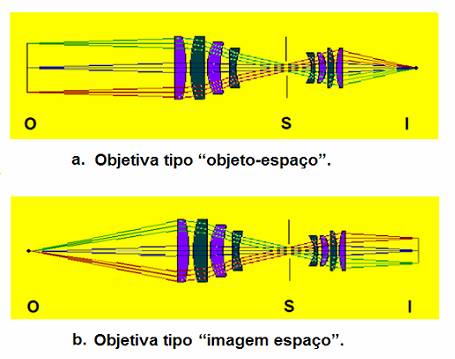
Fig 1a:
Comportamento das objetivas: “objeto-espaço” e“imagem espaço”.
Como dissemos, a característica principal das objetivas telecentricas é que, tanto a pupila de entrada como a pupila de saída encontram-se no infinito. Portanto os raios principais (os raios oblíquos que passam pelo centro da abertura do diafragma *) são paralelos ao eixo óptico à frente e atrás do sistema óptico. A dupla telecentrica terá ambas pupilas no infinito e raios principais em ambos os lados.
* observe na figura 1: Esta dupla telecentrica na realidade corresponde a dois telescópios do tipo Galileu simetricamente dispostos. Estes telescópios possuem diferentes poder de ampliação e isto produz uma variação das ampliações através de feixes paralelos mais ou menos concentrados.
Objetivas normais demonstram variação da imagem dos objetos quando focalizadas. (as antigas objetivas com focalização no elemento frontal, também não apresentam variação do objeto quando focalizam, pois estas diminuem suas focais relativas à medida que focalizam mais próximo.
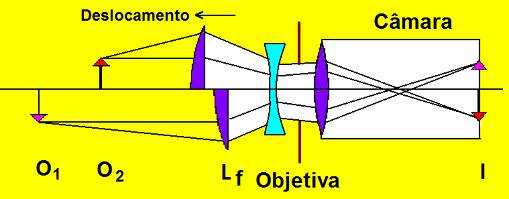
Fig 2
Focalização pelo deslocamento do elemento frontal. A distância objetiva Imagem (I) permanece imutável. Apenas o elemento frontal se desloca para frente ou para trás.
Experimentando a telecentrica
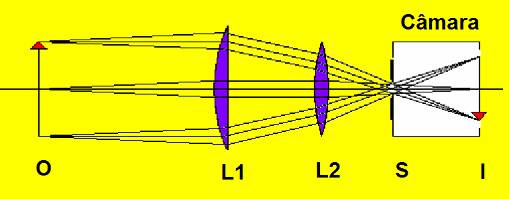
Fig 3
Construindo uma objetiva telecentrica
O= objeto, L1= 1ª lente, L2= 2ª lente, S= diafragma ou objetiva da câmara digital, I= imagem
Você poderá construir uma telecentrica para compreender seu funcionamento. Lembre-se que o princípio é o mesmo de um telescópio. Poderemos usar um do tipo Galileu, como poderemos fazer uso de um do tipo Kepleriano. Este último é mais simples, uma vez que é constituído apenas por lentes convergentes. Na fig 3 vemos L1 como a objetiva do telescópio e L2 como a ocular. E uma pequena câmara digital, ou uma SLR se seu caso for apenas visualizar o fenômeno. A objetiva da câmara S está apenas indicada. O funcionamento seria o mesmo com apenas uma pequena abertura para limitar os raios luminosos a feixes estreitos. Se a câmara for uma de alta qualidade e estiver equipada com uma objetiva de grande abertura (tipo 1.4 ou 1.2), a “ocular” L2 poderá ser dispensada. Se v. conseguir uma lente L1 de grande diâmetro, você terá necessidade de adaptar uma lente negativa da ordem de -2 dioptrias na objetiva da câmara para permitir uma distancia maior entre L1 e o objeto O, favorecendo um maior ângulo de visão. I corresponderá ao plano do filme ou do sensor. Se for usada apenas L1, o ponto focal da mesma deverá coincidir com o Plano do diafragma da câmara (plano S).
A câmara é movida para frente ou para trás em relação ao sistema óptico L1/L2 ou (simplesmente L1) até que a condição de telecentragem seja obtida, isto é, o tamanho do objeto visto pela câmara independe da sua distância em relação a L1. O objeto então é colocado na posição de melhor foco.
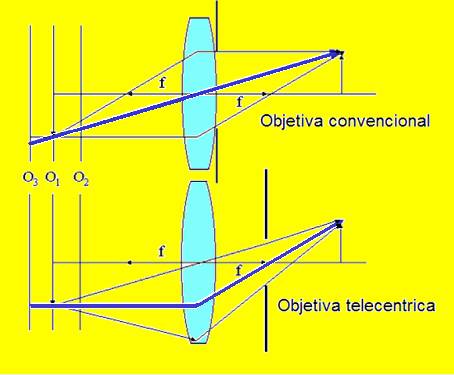
Fig 4
Comparativo entre o traçado dos raios luminosos das lentes convencionais e as telecentriacas para objetos em três posições distintas.
Examinando esquematicamente os Raios Principais (em azul) entre a objetiva convencional e a telecentrica, observamos que existe um diferente trajeto entre ambas. Na primeira, o tamanho do objeto depende da distancia à lente. Assim, para objetos iguais, objetos mais próximos estarão aparentemente maiores. (O Raio Principal está mais perto do eixo óptico) Objetos mais afastados aparecerão menores (O Raio Principal está mais afastado do eixo óptico).
Na óptica telecentrica o Raio Principal torna-se paralelo ao eixo. O detalhe crítico é que a altura do raio relativo ao eixo do sistema permanece constante, indiferentemente da distância entre a lente e os objetos. Desta forma, os objetos permanecem sempre do mesmo tamanho (i.e. ampliação constante) através de todo o campo utilizável. Você, todavia verá que o foco será dependente da distância lente objeto como uma lente comum, mas a imagem permanecerá sempre do mesmo tamanho em qualquer distância entre a lente e objeto. Esta propriedade é útil para reconhecer dimensões em tarefas mecanizadas.
Esta propriedade básica é naturalmente estendida a objetivas mais complexas. Quando temos uma óptica de múltiplos elementos, que é na realmente o que existe no mundo real, um cuidado especial terá que ser tomado para que a pupila de saída da objetiva do sensor seja colocada atrás do plano focal da lente frontal conforme demonstramos na figura a seguir fig 5. O outro grupo de elementos fica situado de tal maneira que a pupila de entrada coincida com a pupila de saída do grupo anterior.
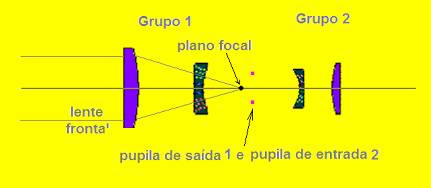
Fig 5
Posicionamento dos grupos ópticos na objetiva telecentrica de acordo com a descrição antrior.
Outra conseqüência interessante notada por Watanabe e Nayar (1996) é que a distância focal efetiva do sistema óptico não varia com a mudança da distância entre o objeto e a objetiva, portanto, dentro do campo de profundidade de foco, não se observa perda de luminosidade nos objetos.

Fig 6
Comparativo entre duas imagens obtidas do mesmo objeto (brinquedo LEGO) . A esquerda com objetiva convencional, à direita com uma telecêntrica.
Muitos de nos estamos familiarizados com a variedade de sistemas ópticos. Um telescópio permite ver coisas distantes em dimensões que poderemos discernir, sem eles, os objetos pequenos passariam desapercebidos. Os telescópios são especificados pelo diâmetro da objetiva. O microscópio nos mostra coisas muito pequenas através da grande aproximação. Os microscópios são especificados pelo seu poder de aumento. As objetivas fotográficas pelas suas aberturas relativas e distancia focal. As lentes usadas na visão máquina (telecentricas) pertencem a esta família. Nestas os raios principais que formam um cone de raios luminosos provindos dos objetos, são manipulados para criar a imagem que desejamos. A manipulação do feixe de raios é indicada em distancia focal f/# e outras.
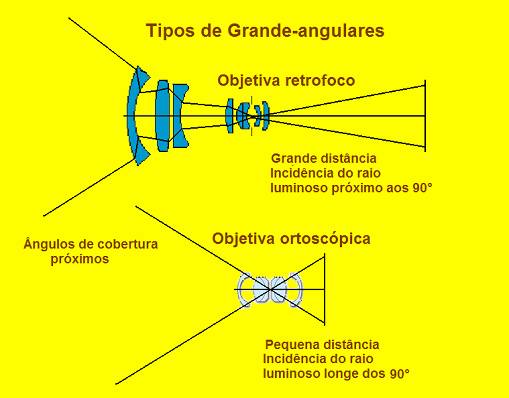
Fig 7
A título comparativo vemos que os raios emergentes (os que chegam ao filme ou ao sensor) são muito inclinados nas lentes ortoscópicas de pequena distancia focal, mas chegando ao paralelo nas objetivas retro focus de mesma focal. As objetivas retrofoco, são na realidade telescópios invertidos e representam o inicio das idéias de telecentragem. Fato é que as perspectivas em ambas diferem algo, mesmo sendo as duas de distâncias focais equivalentes
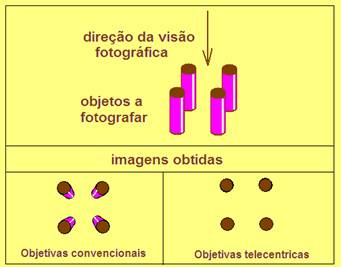
Fig 8
Comparação da perspectiva visual ente as objetivas convencionais e telecentricas ao fotografarem o mesmo objeto. Exemplo clássico da formação de imagem no sistema telecentrico.
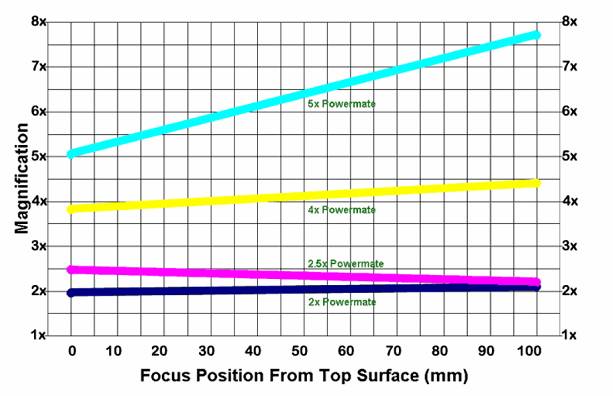
Fig 8a
O gráfico acima corresponde ao comparativo sobre a variação das dimensões de imagem sobre o plano focal de objetos posicionados de 0 a 100mm da parte frontal da objetiva telecentrica. O gráfico é fornecido pela Firma Televue Optics , especialista neste tipo de objetivas. São demonstradas as evoluções de quatro tipos de objetivas “Powermate” a 2X, a 2.5X, a 4X e a 5X. Pelo gráfico acima deduzimos os porquês da figura 8.
As vantagens e limitações das Objetivas Telecentricas.
As objetivas Telecentricas não são afetadas pela distorção de paralaxe. Isto é o ponto de maior interesse para os profissionais da “visão máquina”. Esta propriedade permite ver o fundo de cavidades independentemente da posição no campo de visão.
As objetivas Telecentricas são ideais em aplicações de medida. A telecentricidade desta classe de lentes as torna ideais para uma larga faixa de aplicações na área de medições. Qualquer objeto aparecerá do mesmo tamanho independentemente de sua distância à objetiva, desde que na faixa do campo de visão de uma objetiva telecentrica corretamente projetada. Isto é especialmente útil quando raios paralelos são necessários para sobrepor múltiplas imagens “coesivas#” de uma cena. Desta forma, uma câmara de varredura criará uma imagem precisa mesmo se de comprimento infinito sem qualquer distorção. A utilização das ópticas telecentricas nas câmaras de varredura é a principal utilização deste tipo de objetivas.
#coesivas = imagens que se sobrepõem tais como as camadas RGB de uma cena qualquer.
As objetivas Telecentricas permitem variações em seu ajuste. As objetivas telecentricas não demonstram erro de ampliação dentro do campo de sua profundidade de foco. Isto torna a montagem e a calibração bem menos complexa, se compararmos a objetivas convencionais.
Existem tipos diversos de objetivas Telecentricas. Conforme mencionamos, estas podem ser do tipo objeto-espaço para aplicações dimensionais. São os tipos mais comuns. Podem também ser do tipo imagem-espaço tais como as usadas para medições de profundidade a partir de sua propriedade de focalização muito precisa. Podem ainda ser telecentricas simultaneamente em ambos os lados, tal como num telescópio. Existem porém poucas objetivas telecentricas também zoom. Devemos contudo tomar cuidado em aceitar certas objetivas comerciais ditas como telecentricas e concomitantemente zoom, pois a pupila de saída de qualquer sistema zoom tende a mudar de posição com a ação do zoom, violando assim a condição de telecentragem de uma objetiva.
Informações Importantes das Ópticas Telecentricas
Não seja enganado pelas propagandas das objetivas telecentricas. Estas são as verdades.
As objetivas Telecentricas não oferecem maior profundidade de campo. As objetivas telecentricas estão limitadas a trabalhar dentro das leis da física, exatamente como as ópticas tradicionais. Assim a profundidade de campo aumenta com a diminuição da abertura relativa como é natural; e as telecenticas possuem em geral aberturas relativas muito pequenas, por isto as pessoas pensam que estas objetivas possuem grande profundidade de foco.
As objetivas Telecentricas não são o único meio de realizar medidas precisas. Absolutamente. Dado um paralaxe conhecido este poderá ser mapeado e corrigido. Também uma dada posição ou marcação pode ser determinada num diagrama MV tal que a imagem seja sempre obtida a partir do mesmo ponto. Assim, até mesmo havendo uma distorção na objetiva, se imagens idênticas são conhecidas a partir do mesmo ponto no espaço objeto, poderemos então determinar o valor da distorção.
As objetivas Telecentricas possuem uma visão paralela ao infinito. Todavia, uma lente telecentrica não poderá sozinha corrigir os problemas de iluminação, nem aumentar sua produção. O sistema de visão deve ser projetado com os mesmos cuidados que as lentes padrão convencionais.
A Telecentria não é a única característica importante. As lentes escolhidas sempre dependem de sua resolução, distorção, e outras especificações que afetam suas aplicações.
Um fato pouco desejável, mas conseqüência imediata do objeto a ser registrado, pode ser visualizada na Figura 3 telecentrica, onde o primeiro elemento terá que necessariamente ser um pouco maior que o objeto a ser fotografado (para que o objeto caiba dentro da imagem final), perfazendo assim as condições necessárias de iluminação e telecentragem. Poderíamos, portanto dizer que existe uma real limitação dos objetos a serem fotografados e as lentes deverão ser grandes e adequadamente instaladas para as operações de registro.
Nas objetivas Telecentricas, o campo visual corresponde apenas ao diâmetro da lente frontal. Tais lentes Telecentricas são maiores, mais pesadas e mais caras que as objetivas normais de distância focal e de abertura similares. Isto é devido aos componentes extras que são necessários para alcançar a telecentricidade, e também porque o lado “objeto” da objetiva necessita ser tão grande quanto o objeto a fotografar, ou cuja imagem será formada. Atualmente (2009) estas lentes estão na casa das centenas a milhares de Dólares ou Euros. Em função de suas necessidades, estas lentes devem ter maior resolução e transmitir mais luz à mesma abertura que as objetivas fotográficas normais de uso comercial.
As objetivas Telecentricas são necessárias para evitar a vinhetação e interferência que ocorre na trama de Bayer dos sensores digitais. Para melhorar a qualidade final de imagem estas objetivas são freqüentemente usadas com iluminadores de LED que proporcionam uma iluminação com raios mais paralelos que as fontes convencionais.
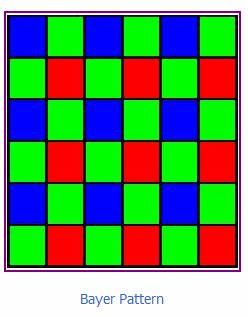
Fig 9
O gráfico de Bayer quanto a disposição dos filtros sobre os sensores dos sistemas digitais.
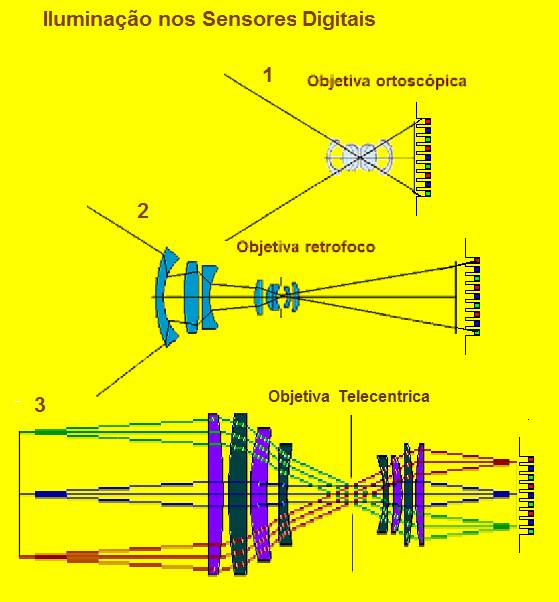
Fig 10
Gráfico de demonstração quanto à iluminação dos sensores digitais tipo CCD (extrema direita). Estes sensores situam-se no final de micro tubos sob s superfície do metal hospedeiro. Desta forma objetivas do tipo ortoscópicas (setor 1) não iluminam as bordas do sensor em seus raios extremos causando a conhecida vinhetação (perda gradual de iluminação em direção aos cantos - discutida na parte 3 deste mesmo trabalho). As objetivas retrofocus (setor 2) produzem uma melhor iluminação, todavia podem ainda causar uma certa interferencia entre as cores (superposição), mas as telecentricas (setor 3) são ideais para este tipo de sensor.
Nas objetivas Telecentricas estaremos trabalhando em outros parâmetros que diferem em muito das objetivas convencionais.

Fig 11
A tabela acima, editado pelo fabricante Moritex representa as especificações de quatro versões de objetivas telecentricas para medição gráfica. A primeira possui 2x de aumento fixo a segunda 4x a terceira 6x a quarta 8x. Estes valores correspondem à relação final do gabarito -Tamanho da imagem/ Tamanho do Objeto. Nesta tabela de características semelhantes aos de outros fabricantes veremos: FNO= f number ou aberura relativa. A mais luminosa possui f/14.7 e amenos luminosa f/57.3. Esta é a primeira das grandes limitações. Eexige grande quantidade de luz para fornecer uma boa imagem; O/I corresponde a relação de distâncias OS/SI demonstradas na figura 1a, para a melhor qualidade final de imagem. WD Widest Diameter, corresponde ao maior diâmetro da lente frontal, que é também o campo abrangente de imagem registrável; Depht of Field ou espessura, profundidade de foco em que não há percepção de perda de qualidade na imagem registrada. (este ponto já foi discutido em nosso trabalho nas figuras do Anexo 2 e na neste mesmo trabalho em sua parte 3); Resolution corresponde a mínima espessura de linhas capaz de ser desenhada pela objetiva, quando em presença de raios UV cuja freqüência não é especificada. TV distortion é o percentual de distorção medido em uma tela de televisão supostamente plana, dada pela alteração de distância entre duas linhas paralelas medidas entre o eixo vertical central e o eixo vertical extremo nesta tela considerada padrão. NA ou numerical aperture é o diâmetro em mm das pupilas internas dos blocos ópticos que compõem a objetiva; Peso em gramas e o maior diâmetro de sensor compatível são os dados das ultimas colunas.
Os dados não mentem. Tudo é questão de interpretação. Por eles vemos as limitações de uso geral destas objetivas. Em primeiro lugar sua falta de luminosidade, em seguida o campo limitado de distâncias pelo que elas são destinadas.

Fig 12
Objetivas Telecentricas de diversos fabricantes.
As objetivas Telecentricas não servem como teleobjetivas. Imagine que registrando apenas a imagem correspondente ao diâmetro da lente frontal, teríamos poderosíssimas telefotos para captar pequenos detalhes a grandes distâncias. Mas aqui entram as leis da física que estabelece que a resolução de um objeto visualizado por uma óptica é proporcional ao exponencial do inverso da distância da objetiva ao objeto. Por esta mesma razão, e pelo fato de manter as dimensões praticamente imutáveis, a qualidade se deteriora rapidamente, limitando tais objetivas a um campo visual bastante restrito.
xxxxxxxxxxxxxxxxxxxxxxx
Lentes de espelho
Introdução
Este é outro entre os tipos que diferem do tradicional. Poucas pessoas ouviram falar nelas. Algumas décadas atrás era um assombro. Muitos fabricantes as produziram em focais de 250 mm. a 2000 mm. E até mais. Todas se baseiam em uma antiga invenção. O telescópio de Newton. Aqui complementamos nossa Base Geral da Terminologia Óptica 4.
Em 1670 Sir Isaac Newton, apresentou os detalhes de seu telescópio de espelhos a Royal Society, tendo-o incluído em sua obra “Opticks”, somente em 1704, quando seu projeto tornou-se de conhecimento público. Na verdade, a idéia de substituir os vidros por espelhos com o intuito de melhorar a qualidade da imagem através da supressão da irisação, (aberração cromática) tão comum nas ópticas da época, já havia sido estabelecida pelo matemático escocês James Gregory, que já havia construído um tipo similar em 1640.
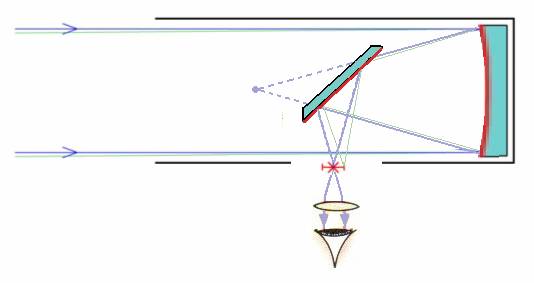
Fig 1
Telescópio de Newton.
Foi porém o padre francês, professor do famoso colégio Pocquet de Chartres (França), Laurent Cassegrain (1629-1693) que em 1672 desenhou e construiu o primeiro telescópio com espelho primário côncavo vazado com espelho secundário de grau, que permitia visualizar a imagem pelo eixo óptico. Este telescópio não produzia boas imagens, mas demonstrou que era possível construir um telescópio fisicamente curto e com grande abertura luminosa para aquele tempo. O projeto de Cassegrain tornou-se a base de quase todos os telescópios de espelho atuais.
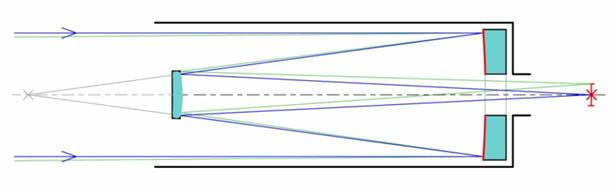
Fig 2
Telescópio de Cassegrain
O Cassegrain "Clássico"
Naquela época não havia câmaras fotográficas. Quando elas passaram a existir o telescópio de espelho foi logo aproveitado. No desenho "Classico" de Cassegrain o espelho primário é parabólico e o secundário é hiperbólico e este reflete os raios luminosos pela abertura do espelho primário. O dobramento dos raios permite um desenho compacto. Os espelhos secundários podem ser planos em telescópios de baixo aumento, como era o caso das objetivas Kanko-2600, fabricada nos anos 1940. Em alguns casos o espelho secundário é montado num vidro plano, o que favorece a não formação de imagens com raios ou tipo aranha causadas por suportes mecânicos usados em alguns modelos. Quando montado em vidros, este favorece a proteção contra a poeira e riscos no espelho apesar de haver uma pequena perda de luminosidade.
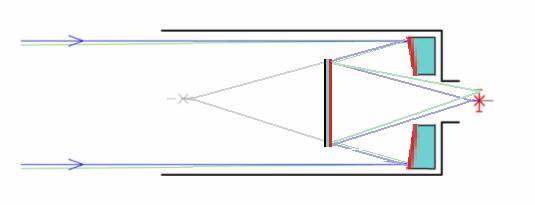
Fig 3
Telescópio “Kanko-2600”
Do funcionamento
O espelho parabólico côncavo refletirá todos os raios emergentes paralelos ao eixo óptico em um único ponto de foco. O refletor hiperbólico convexo tem dois pontos de foco e este sempre refletirá todos os raios direcionados a um de seus focos, em direção ao outro. Os espelhos deste tipo de telescópio são projetados e posicionados de tal forma a compartilhar um dos focos (o foco interno do espelho hiperbólico), de modo que o segundo foco esteja no mesmo ponto em que a imagem será observada, normalmente no foco da ocular, ou no plano do filme. Resumindo: O espelho parabólico reflete os raios luminosos paralelos para o seu foco que também é um dos focos do espelho hiperbólico. Este então reflete em seu outro foco a imagem a ser observada.
O telescópio de Cassegrain possui uma série de variantes que vamos aqui descrever. È interessante observar que este invento do inicio do século XVII só recebeu seus primeiros aperfeiçoamentos no início do século XX, ou seja, quase trezentos anos depois.
Ritchey-Chrétien
O telescópio Ritchey-Chrétien foi a sua primeira reformulação. Foi inventado por George Willis Ritchey (1864-1945) e Henri Chrétien (1879-1956) com o auxílio construtivo de George H. Lutz, nos início dos anos 1910. Mantendo o mesmo desenho geral, este possui dois espelhos hiperbólicos (no lugar do parabólico primário e um hiperbólico secundário). É, portanto livre de coma e aberrações esféricas e possui um plano focal plano, portanto com qualidades mais apreciáveis que o desenho tradicional, tornando-o ideal para observações em campo amplo e usos fotográficos. Praticamente todos os telescópios refletores profissionais em uso nos observatórios astronômicos mundiais são deste tipo. Tais como os telescópios gigantes e os telescópios gêmeos de 10 metros do Observatório de Keck.
O Prof. Henri Chrétien também desenvolveu a
base geral da projeção em tela ampla com as lentes Hypergonar em 1927 que foi o
precursor o Cinemascope. Veja em Base Geral da Terminologia Óptica 6.
Dall-Kirkham
O projeto de Dall-Kirkham foi criado por Horace Dall em 1928 e tomou este nome devido a um artigo publicado na revista Scientific American em 1930 devido a uma contenda entre o astonomo amador Allan Kirkham e o editor da revista Albert G. Ingalls naquela época. Este telescópio usa um espelho primário côncavo de forma elíptica e um espelho secundário convexo esférico. Apesar de ser de mais fácil construção que o modelo Cassegrain clássico e que o tipor Ritchey-Chretien, este não corrige o coma fora de eixo nem a curvatura de campo, degradando rapidamente a imagem fora de eixo. O fato de ser usado em grandes focais minimiza os erros, porém limita sua abertura a f/15.
O Desenho Dall-Kirkham Modificado ou Wynne-Rosin. Utiliza a mesma configuração anterior (espelho primário elíptico e espelho secundário esférico), mas inclui duas lentes a frente de seu ponto focal para melhorar a qualidade da imagem fora do eixo. A constante cônica¨¨ é diferente dos Dall-Kirkham convencionais e deve ser otimizada durante a construção. Os campos de utilização são maiores que num telescópio Ritchey-Chretien e em ampla banda do espectro. Tipicamente 0.38 to 0.95 mícron se o corretor é feito de quartzo.
¨¨constante cônica é um numero que avalia as seções cônicas. É representado por K e é função da excentricidade da seção cônica.
K = − e2, .............................................................................Fórmula 1
Estes telescópios foram projetados por Seymour Rosin e Wynne em 1949 após a 2ª Guerra Mundial. Comportam-se de forma igual, ou melhor, que um telescópio Ritchey-Chretien, pois corrige também o astigmatimo. O espelho secundário pode ser testado pelo sistema de franjas no calibre esférico, ou testados por trás. Isto é uma vantagem marcante sobre o espelho secundário hiperbólico ou o Ritchey-Chretien. Alguns observatórios usam esta combinação.
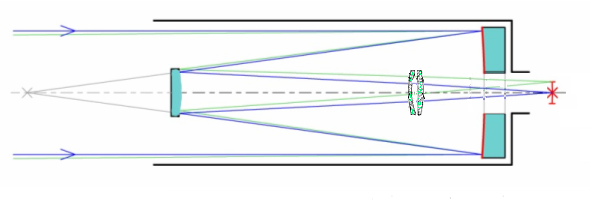
Fig 4
Dall-Kirkham Modificado ou Wynne-Rosin
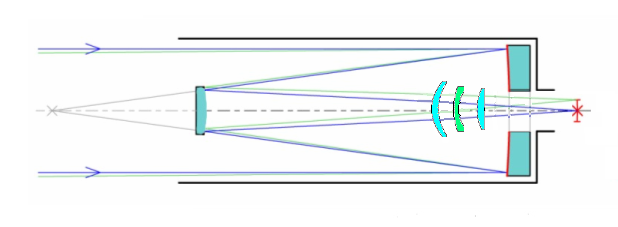
Fig 4a
Wynne-Rosin aperfeiçoado
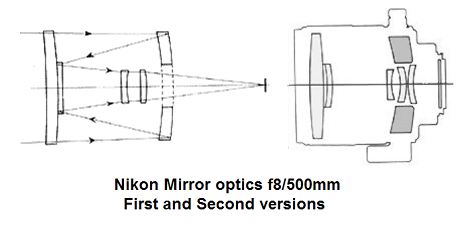
Fig 4b
As objetivas fotográficas 8/500 Nikon de primeira e segunda geração são baseadas nas duas gerações do projeto Wynne-Rosin.
Schiefspiegler
Uma variação estanha com um nome estranho. O nome não é de nenhum autor. Schiefspiegler significa em alemão “de espelho deslocado”. Usa espelhos inclinados para evitar o desenho das sombras do espelho primário no secundário conhecido como “bright-donuts” nos pontos de alta iluminação e fora de foco. (São as “mini rosquinhas” brancas que incomodam na imagem das lentes de espelho). Contudo, este procedimento, apesar de eliminar este inconveniente, nos leva a outras aberrações que devem ser eliminadas.

Fig 5a

Fig 5b
Nesta fotografia de Spystyle (acima - fig 5a) e Douglas Smith (abaixo - fig 5b) visualizamos os anéis causados pelas objetivas de espelho com eixo de visão coincidente ao eixo óptico.
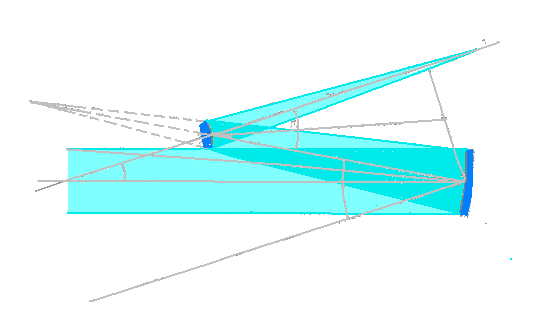
Fig 6a
Esquema do telescópio Schiefspiegler
Um exemplo de utilização da idéia é a objetiva fotográfica Katoptaron de Makowsky
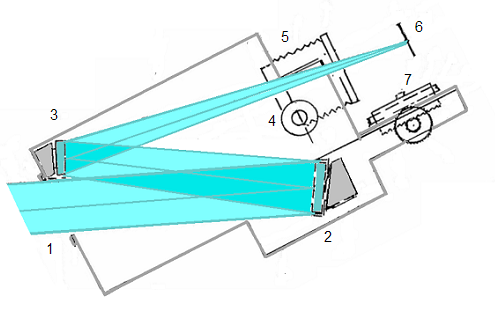
Fig 6b
Objetiva Katoptaron de Makovsky
1= entrada de luz formadora de imagem; 2=primeiro espelho; 3=segundo espelho; 4=comando do diafragma; 5=fole compensador para qualquer registro de montagem; 6=plano do filme; 7=carro de montagem da câmara e focalização.
Telescópio Schmidt
O astrônomo alemão Bernard Schmidt construiu in 1930 uma objetiva de espelho aperfeiçoada com uma lente convergente à frente do sistema óptico. Este método torna possível a construção de um telescópio com angulo de visão de até 15 graus sem qualquer aberração esférica.
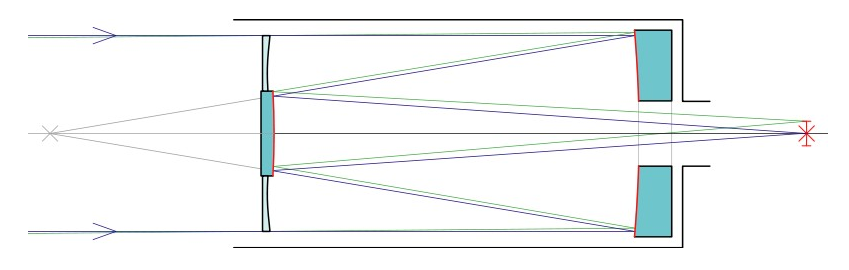
Fig 7
Telescópio de Schmidt
Telescópio Maksutov
Enquanto no projeto Schmidt a lente positiva frontal necessitava ser uma lente asférica de difícil construção, O Dr. Dimitrii Dmitrievich Maksutov do Instituto Optico de São Petersburgo (Russia) publicou no Journal of the Optical Society of America (Vol. 34, No. 5 - May 1944) um novo projeto do telescópio Cassegrain de sua autoria. Ele colocou em frente ao sistema óptico uma lente esférica menisco positivo com a concavidade para frente que neutralizava muitas aberrações. Nascia assim o telescópio Maksutov-Cassegrain. Estas lentes passaram a ser conhecidas como MTO (Meniscus-Tele-Optik).
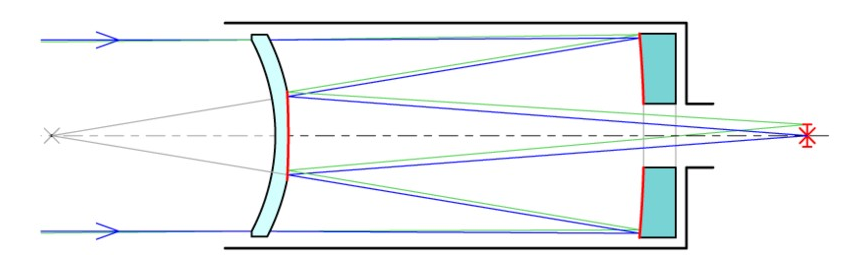
Fig 8
Projeto Maksutov
Seguiram outros aperfeiçoamentos.
No telescopio Argunov-Cassegrain todas as ópticas são esféricas, e o clássico espelho secundário do telescópio Cassegrain é substituído por três lentes com espaço de ar (não coladas). O elemento mais afastado no espelho principal é o espelho de Mangin##, no qual o último elemento atua como um espelho de segunda superfície possuindo a face espelhada voltada para o objeto.
Os sistemas Argunov empregam apenas superfícies esféricas e evitam as dificuldades práticas de produzir e testar superfícies asféricas. Contudo, este benefício não é tão grande pois continua sendo difícil produzir uma área esférica com raio de curvatura de alta precisão necessária para o perfeito funcionamento da unidade.
## Em óptica o espelho de Mangin é uma lente com uma de suas faces espelhada (Sistema catadióptrico). Consiste em uma lente côncava com sua face traseira espelhada. Os espelhos Mangin são usados em sistema de iluminação, tais como nos farois de automóveis e em alguns tipos de telescópios, entre os quais os Klevtsov-Cassegrain e o Argunov-Cassegrain.
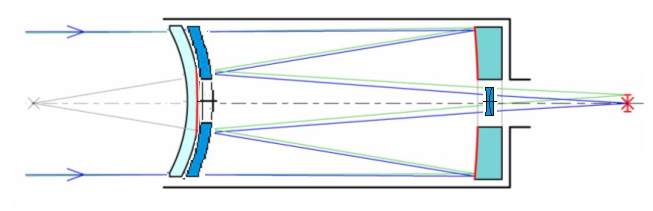
Fig 9a
Esquema MTO 1000
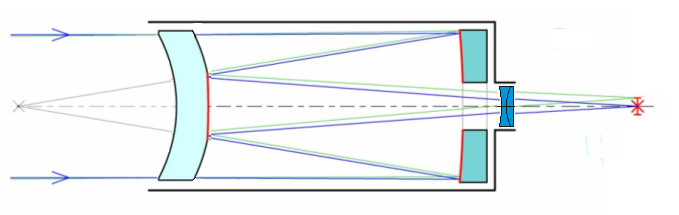
Fig 9b
Esquema MTO500
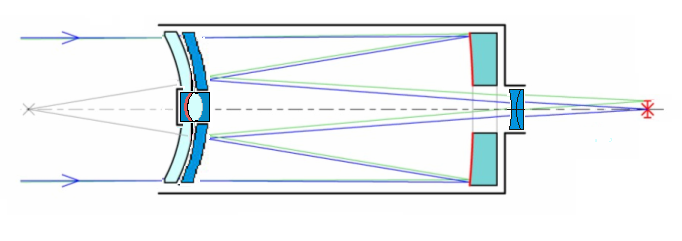
Fig 9c
Esquema Rubin
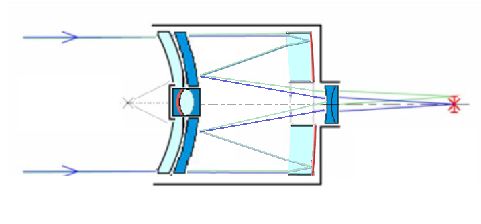
Fig 9d
Esquema Rubin com espelho Mangin
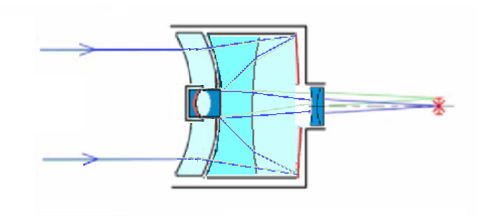
Fig 9e
Uma outra variação também com espelho Mangin, mas construída sem espaços vazios foi a “Solid Cat” desenvolvida nos anos 1970 pelos Laboratórios Perking-Elmer e produzida pela Vivitar. A presença de vidro no espaço aéreo reduzia ainda mais a objetiva, mas proporcionava um peso extra e um custo mais elevado.
Alguns anos antes um cientista holandês e
diretor geral as companhia ´Olddelft - De Oude Delft´ Optical Industry em Delft,
Holland, (1941 - 1968), resolveu colocar dois meniscos colados de diferentes
classes de vidro com idênticos índices de dobramento dos raios luminosos
neutralizando portanto as aberrações cromáticas e não introduzindo qualquer
dioptría ao sistema. O
grupo óptico servia apenas para reorientação dos raios luminosos de entrada.
Albert Bouwers (1893-1972) também
desenvolveu a Câmara Philips para micro fotografia em raios X e o sistema de
espelhos para projeção Super Technorama-7 e Delrama. O primeiro foi utilizado
nas filmagens do desenho animado “A Bela Adormecida” por Walt Disney em 1959.
Veja em: Base Geral da Terminologia Óptica 6.
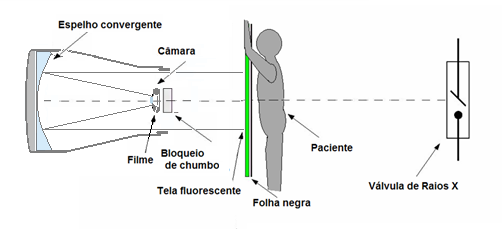
Fig 10
Esquema Câmara Philips de Albert Bouwers. O espelho convergente é a objetiva da câmara. Em posição reversa e com a placa de chumbo bloqueadora para proteger o filme extra sensível. A câmara com obturador próprio vê a tela fluorescente com a imagem do paciente iluminado pelos Raios X sem contudo recebê-los diretamente. O espelho convergente propicia uma grande abertura numérica da ordem de f/0,65, sem aberrações cromáticas. O filme é “green sensitive” e tem uma sensibilidade da ordem dos 5000 ASA/ISO, permitindo exposições muito curtas. O projeto da câmara tem semelhança com a câmara Schmidt para fotografia astronômica.
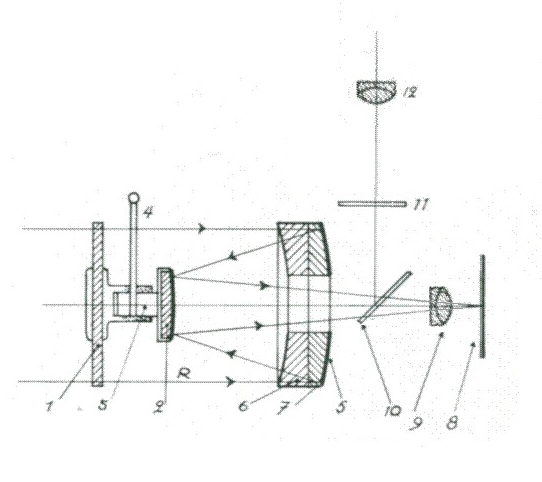
Fig 11
Objetiva Fototel/Miroplar de Bowens
1=vidro plano; 2=espelho secundário; 3= helicóide de focalização; 4=comando de foco; 5=espelho principal; 6 e 7= doublet acromático -índice zero dioptrias- sobre o espelho principal- Espelho Mangin; 8=plano do filme; 9=lente de Barlow ampliadora; 10= espelho para visão axial; 11=tela de focalização; 12= ocular.
Nota: em algumas versões, O vidro plano 1 poderá ser substituído por um vidro com a concavidade para fora com índice de zero dioptrias. Neste caso o espelho 2 é colado ao mesmo e a focalização faz-se pelo deslocamento de toda a unidade frontal.
Projeto do Autor.
O autor resolveu também “brincar” de inventor e desenvolveu uma nova versão de objetiva de espelhos. Tendo experimentado praticamente todos os tipos existentes no mercado, Procurou realizar um novo projeto que não a causasse fadiga visual e física a que estamos acostumados com os telescópios convencionais encontrados no mercado. Astrônomos amadores ficam horas a fio observando os astros. O fato é que todos estes telescópios, do mais barato ao mais caro, introduzem vibrações insuportáveis além de exigirem um grande contorcionismo por parte do observador. Estes problemas haviam de certa forma já sido solucionados para os grandes telescópios usados em observatórios astronômicos. O observador fica numa gôndola dentro do telescópio no seu plano focal, as vibrações passam a ser quase inexistentes, pois estes gigantescos telescópios tem como sua estrutura a mesma do prédio do observatório, ou melhor ainda em alguns casos são até enterrados no solo. Em busca de uma solução para um produto de pequeno porte, encontrou na arquitetura do olho a grande saída. A esfera é isobárica – isto é –mantém seu equilíbrio em qualquer posição. É menos sujeita a vibrações quando adequadamente posicionada, e é essencialmente ergométrica por ser uma forma natural em si mesma. O sistema portanto dispensa o incomodo tripé e pode por si mesma ser colocada em qualquer posição. Adequamos então o principio Maksutov de ultima geração a uma observação a 90° inspirada no telescópio de espelhos do teodolito Wild DKM-3. Nasceu o lTStarlinnTl!
Os protótipos construídos surpreenderam pela qualidade de imagem e estabilidade, propiciando não apenas observações astronômicas, mas também observações terrestres que além de mais estáveis são também mais discretas não só pela compacticidade do instrumento em si mas Na compacticidade gerada pelo sistema óptico-observador que ocupa menos espaço físico que qualquer outra disposição de qualquer outro instrumento: O fato de ser possível o acoplamento de qualquer câmara para registro de imagem aliada a discrição do conjunto também adequa o projeto também ao uso militar e policial. O projeto permitiu construir uma esfera de apenas 23cm em seu diâmetro exterior abrigar uma objetiva de 1150mm! Um fator de redução 1/5! E ainda elimina a necessidade do tripé, da cabeça azimutal etc. A montagem se faz simplesmente sobre um pequeno pneu maciço.
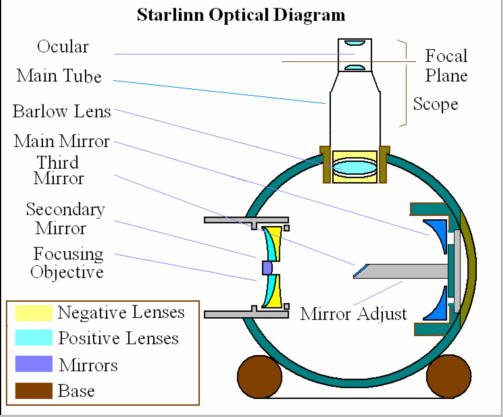
Fig 6
Esfera Telescópica do Prof. Paracampo
Telescópio tipo Maksutov com raios centrais desviados. Propicia observação e registro de imagem sem utilização de tripés ou suportes especiais. Por possuir peso equilibrado, torna-se estável em qualquer posição
Conclusões Gerais.
O funcionamento de todos os sistemas ópticos de espelho segue praticamente o mesmo princípio. Um corpo cilíndrico tem uma lente frontal de grande diâmetro que possui um disco em seu centro. Este é o espelho secundário. Na parte traseira está o espelho principal que é o responsável pela formação da imagem. A distância focal deste, determina a focal da objetiva final. Grandes luminosidades exigem tubos de montagem de grande diâmetro.
Os fabricantes dizem que estas lentes podem ser manualmente usadas, mas o fato que grandes focais (acima dos 500mm) são pesadas e de difícil sustentação. Por isso é sempre recomendável que sejam usadas com suporte apropriado.
Sua aberturas relativas entre 5 e 11 aliadas a um peso razoável, que pode chegar aos 10 kg exige um tripé também pesado e rígido. Em curtas distâncias, a profundidade de foco reduzida também dificulta sua utilização. O efeito dos pontos quentes e os anéis que forma na imagem fora de foco, as “rosquinhas” discutidas anteriormente, são também um fator de distúrbio visual. A lente de espelho não possui aberração cromática e isto facilita grandes ampliações da imagem. Outras vantagens são a maior passagem de luz por não haver absorção por parte dos vidros, causando, portanto maior contraste na imagem, e a dispensa de correção para a onda do infravermelho.
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
Temperatura de cor
Porque medimos as matizes da luz como "temperatura"? Isto começou no final dos anos 1800s, quando o físico Inglês William Kelvin decidiu aquecer um bloco de carvão. Este brilhava no calor, produzindo uma gama de diferentes cores a diferentes temperaturas. O cubo negro que a princípio produzia uma diminuta luz vermelha aumentava para um amarelo brilhante enquanto a temperatura subia, e chegava a produzir até um brilho azul esbranquiçado nas temperaturas mais altas. Em sua honra, as Temperaturas de Cor são medidas em graus Kelvin, que vem a ser uma variação dos graus Centígrados (ou Celsius). Ao invés de partir da temperatura onde a água congela, a escala Kelvin inicia no "zero absoluto", que ocorre a -273 graus Centígrados. (Subtraia 273 da temperatura Kelvin e V. terá o equivalente in Centígrados.) Contudo, as temperaturas de cor atribuídas a diferentes tipos de luz correspondem apenas às cores visíveis que se equivalem ao corpo negro padrão, e não à verdadeira temperatura na qual se encontra o filamento da lâmpada.
Natureza da luz
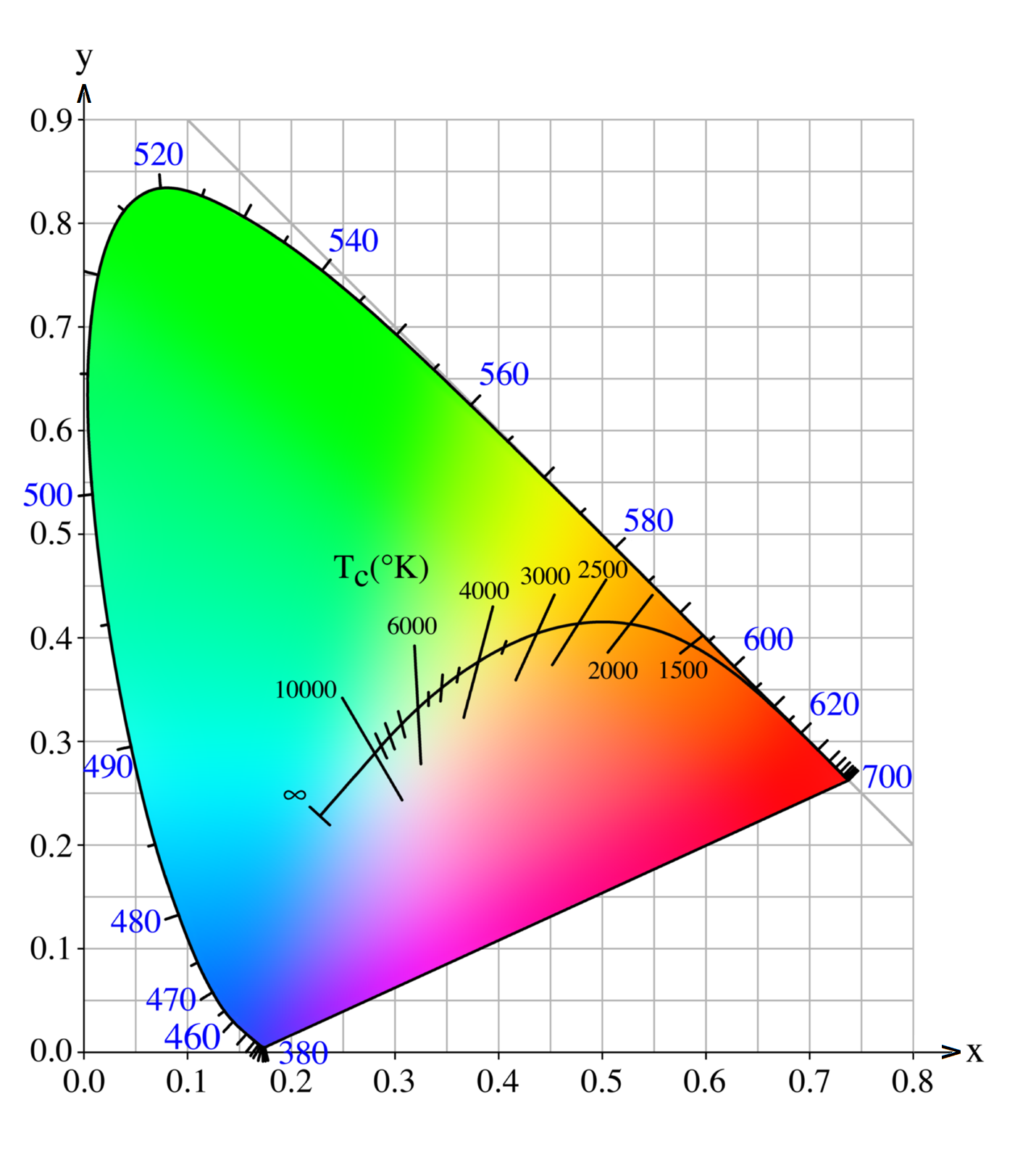
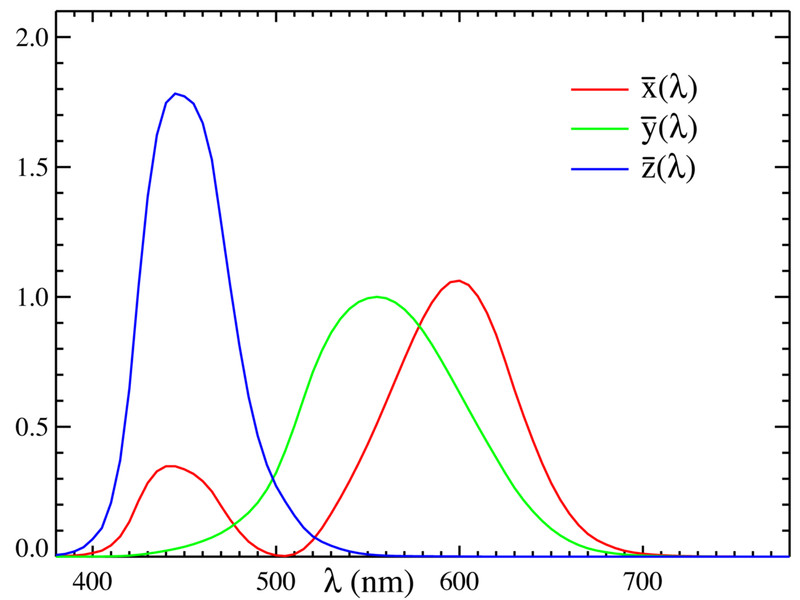
O espaço de cromaticidade x,y, CIE 1931, mostra as cromaticidades provindas das emanações luminosas de um corpo negro em suas várias temperaturas (Planckian locus), e as linhas das constantes de equivalência da temperatura de cor.
Na teoria da cor, o Planckian locus é geralmente o trajeto ou o locus que a cor de um corpo negro percorreria num particular espaço de cromaticidade (espaço de cor) determinado pelas mudanças de temperatura no corpo negro. Normalmente, o espaço de cromaticidade é composto por três números (X, Y, e Z, por exemplo) correspondente ao conheido diagrama vetorial espacial de três eixos. Estes especificam a cor e o brilho de um estímulo visual homogêneo. Às vezes nós queiramos apenas tratar da cromaticidade (cor) de um determinado estímulo visual. Este é um espaço bidimensional de dois números (x e y) que dispensam a informação do brilho. Neste caso o Planckian locus é o trajeto que a cor de um corpo negro percorre neste diagrama de espaço de cromaticidade ao sofrer as diversas mudanças de temperatura.
A Temperatura da Cor é uma medida em graus Kelvin que indica a matiz de um tipo específico da fonte luminosa. Você pode usar uma temperatura de cor (segundo as indicações da tabela abaixo) para sugerir cores realísticas para as luzes em uma cena 3D.
As cores visíveis são relativas ao Balanço de Cor (ou ao Balanço de Branco) de um estoque de película ou de uma câmara de vídeo, com os dois ajustes fixos os mais comuns que são o balanço da cor para interiores em 3200K, e ao balanço da cor para ao ar livre 5500K (da luz do dia). Para escolher um valor do RGB da carta abaixo, escolha primeiramente se sua cena estaria realizada com película para interiores ou para ar livre (escolhida geralmente baseado na iluminação dominante), a seguir encontre a cor corresponder ao tipo de fonte luminosa nessa cor.
Luz de um dia nublado 6.000/7000 ºK
Luz de um dia com o céu limpo 5.500 º K
Luz incandescente de quartzo/halogênio 3200 ºK
Luz incandescente doméstica 2000 ºK
Não poderíamos encerrar este tópico de orientação sem nos referirmos aos lasers que são fontes de luz monocromática de forma mais absoluta. Esta é obtida através da ressonância atômica dos diversos elementos usados como base. Estas luzes são ditas como “coerentes”, isto é, além de serem todas da mesma freqüência, estão todas sempre na mesma fase.
Tabela de Referencia
Os números comumente usados estão abaixo incluídos:
|
número Wratten |
Cor |
Fator do Filtro |
Usos e características |
|
1A |
|
|
Chamado de filtro skylight, absorve a radiação ultravioleta, e reduz a névoa na fotografia de paisagem. |
|
2A |
Amarelo pálido |
|
Absorve a radiação ultravioleta. |
|
2B |
Amarelo pálido |
|
Absorve a radiação ultravioleta,ligeiramente menos que #2A. |
|
2C |
|
|
Absorve a radiação ultravioleta. |
|
2E |
Amarelo pálido |
|
Absorve a radiação ultravioleta, ligeiramente mais que #2A.. |
|
3 |
Amarelo claro |
|
Absorve o azul excessivo do céu, tornando-o ligeiramente mais escuro em imagens preto e branco. |
|
4 |
Amarelo |
|
|
|
6 |
Amarelo claro |
|
|
|
8 |
Amarelo |
2 |
Absorve mais azul que #3. |
|
9 |
Amarelo profundo |
|
Absorve mais azul que #8. |
|
11 |
Amarelo esverdeado |
|
Correção de cores. |
|
12 |
Amarelo profundo |
|
Filtro azul-negativo; complementam o #32 verde-negativo e o #44A vermelho-negativo. Usado com Ektachrome ou Aerochrome do tipo Infravermelho obtemos resultados de falsas cores. |
|
15 |
Amarelo profundo |
|
Faz com o céu fique escuro em fotografia preto e branco em exteriores. |
|
16 |
Amarelo Laranja |
|
Como #15, mas mais forte. |
|
21 |
Laranja |
|
Filtro de contraste absorve o azul e o azul-verde. |
|
22 |
Laranja profundo |
|
Filtro de contraste, efeito mais forte que #21. |
|
23 |
Vermelho claro |
|
|
|
24 |
Vermelho |
|
|
|
25 |
Vermelho tricolor |
|
Usado em separação de cores e fotografia infravermelha. |
|
26 |
Vermelho |
|
|
|
29 |
Vermelho profundo |
|
Usado em separação de cores, complementa #47 e #61. em preto e branco faz com o céu fique bem escuro, quase negro. Em fotografia infravermelha, bloqueia a maior parte da luz visível aumentando o efeito do infravermelho na cena. |
|
32 |
Magenta |
|
Verde-negatvo. Complementa o #12 azul-negativo e o #44A vermelho-negativo. |
|
34A |
Violeta |
|
Usado para separação verde-negativo e azul-positivo. |
|
38A |
Azul |
|
Absorve o vermelho, algum UV algum verde da luz. |
|
44 |
Azul -Verde claro |
|
Vermelho-negativo com muita absorção de UV. |
|
44A |
Azul -Verde claro |
|
Vermelho-negativo, complementa o #12 azul-negativo e o #32 verde-negativo. |
|
47 |
Azul tricolor |
|
Usado para separação de cores. Complementa o #29 e o #61. |
|
47A |
Azul claro |
|
Ao remover luzes que não sejam azuis, os objetos azuis e púrpuros mostram uma maior variedade de meios tons. É usado em aplicações médicas que envolvem matizes de fluorescência. |
|
47B |
Azul profundo tricolor |
|
Separação de cores. |
|
50 |
Azul profundo |
|
|
|
56 |
Verde claro |
|
|
|
58 |
Verde tricolor |
|
Separação de cores. Ao remover as luzes não verdes, os objetos verdes tais como a folhagem, mostram uma maior variedade de nuances. |
|
61 |
Verde profundo tricolor |
|
Separação de cores complementa os filtros #29 e #47. |
|
80A |
Azul |
4 |
Conversor de cores. Eleva a temperatura de cor propiciando que uma cena iluminada a 3200 K (tungstênio) apareça como se fosse iluminada pela luz do dia aproximadamente 5500 K. Isto permite que uma película balanceada para luz do dia seja usada com lâmpadas de tungstênio. |
|
80B |
Azul |
3 |
Similar ao 80A; converte 3400 K a 5500 K. |
|
80C |
Azul |
2 |
Similar ao 80A; converte 3800 K a 5500 K. Tipicamente usado com lâmpadas de flash brancas e películas do tipo luz do dia. |
|
80D |
Azul |
1.5 |
Similar ao 80A; converte 4200 K a 5500 K. |
|
81A |
Laranja pálido |
1.4 |
Filtro de aquecimento para aumento ligeiro da temperatura de cor; Pode também ser usado quando filmando com película para tungstênio tipo B (3200 K) com lâmpadas photoflood de 3400 K. O oposto do 82A. |
|
81B |
Laranja pálido |
1.4 |
Filtro de aquecimento ligeiramente mais forte que o 81A. O oposto do 82B. |
|
81C |
Laranja pálido |
1.5 |
Filtro de aquecimento ligeiramente mais forte que o 81B. O oposto do 82C. |
|
81D |
Laranja pálido |
|
Filtro de aquecimento ligeiramente mais forte que o 81C. |
|
81EF |
Laranja pálido |
|
Filtro de aquecimento mais forte que o 81D. |
|
82A |
Azul pálido |
1.3 |
Filtro de esfriamento para abaixar ligeiramente a temperatura. O oposto do 81A. |
|
82B |
Azul pálido |
1.4 |
Filtro de esfriamento, ligeiramente mais forte que o 82A O oposto do 81B. Pode também ser usado quando filmando com película para tungstênio tipo B (3200 K) com lâmpadas domésticas de 100W (2900 K). |
|
82C |
Azul pálido |
1.5 |
Filtro de esfriamento, ligeiramente mais forte que o 82B O oposto do 81C. |
|
85 |
Âmbar |
3 |
Conversor de cores, o oposto do 80A; este é um filtro de aquecimento; transforma uma cena de ar livre iluminada pelo sol (temperatura de cor ao redor de 5500 kelvins) parecer como iluminada por lâmpada incandescente de tungstênio (temperatura de cor ao redor de 3400 K). Permitindo películas balanceadas para interiores serem usadas ao ar livre. |
|
85B |
Âmbar |
3 |
Similar ao 85; converte 5500 K a 3200 K. |
|
85C |
Âmbar |
1.5 |
Similar ao 85; converte 5500 K a 3800 K. |
|
85N3 |
Âmbar |
|
Densidade neutra de 1 ponto + Conversor de cores, to oposto do 80A; é um filtro de aquecimento que transforma cenas de ar livre iluminadas pelo sol (temperatura ao redor de 5500 kelvin) parecerem iluminadas por lâmpadas de tungstênio (temperatura ao redor de 3400 kelvin). Permitindo películas balanceadas para interiores serem usadas ao ar livre. |
|
85N6 |
Âmbar |
|
Densidade neutra de 2 pontos + Conversor de cores, to oposto do 80A; é um filtro de aquecimento que transforma cenas de ar livre iluminadas pelo sol (temperatura ao redor de 5500 kelvin) parecerem iluminadas por lâmpadas de tungstênio (temperatura ao redor de 3400 kelvin). Permitindo películas balanceadas para interiores serem usadas ao ar livre. |
|
85N9 |
Âmbar |
|
Densidade neutra de 3 pontos + Conversor de cores, to oposto do 80A; é um filtro de aquecimento que transforma cenas de ar livre iluminadas pelo sol (temperatura ao redor de 5500 kelvin) parecerem iluminadas por lâmpadas de tungstênio (temperatura ao redor de 3400 kelvin). Permitindo películas balanceadas para interiores serem usadas ao ar livre. |
|
87 |
|
|
|
|
87C |
Opaco |
|
Deixa passar os infravermelhos porem não as freqüências visíveis. |
|
89B |
Quase-opaco |
|
Deixa passar os infravermelhos porem não as freqüências visíveis abaixo de 720 nm (vermelhos muito escuros). Usa-se em fotografia aérea. |
|
90 |
Cinza escuro-Âmbar |
|
Usado para visão das cenas sem cores antes de serem fotografadas. |
|
92 |
Vermelho |
|
Densitometria de cores. |
|
96 |
Cinza |
variável |
Filtro de densidade neutra. Bloqueia todas as freqüências da luz igualmente, tornando a cena mais escura. Disponíveis em vários valores distinguíveis pela densidade ou fator de filtro. |
|
98 |
Azul |
|
Equivalente a soma dos filtros #47B + #2B. |
|
99 |
Verde |
|
Equivalente a soma dos filtros #61 + #16. |
|
102 |
Amarelo-Verde |
|
Conversor de Cores; cria uma barreira de forma que as fotocélulas respondam como o olho humano. |
|
106 |
Âmbar |
|
Conversor de Cores; faz com que as fotocélulas do tipo S-4 respondam como o olho humano. |
POLARIZADORES
E
POLARIZAÇÃO DA LUZ
CÉLULA DE KERR
CÂMARA RAPATRONIC
Fonte:
The Center for Occupational
Research and Development
601 C Lake Air Drive
Waco, Texas 76710
Tradução e adaptação:
L. Paracampo
DEFINIÇÕES
A luz não polarizada consiste em vibrações de onda em muitos sentidos perpendiculares ao sentido do seu curso.
Um elemento polarizador é então, um dispositivo que filtra, elimina ou obstrui todas as vibrações, exceto aquelas num plano desejado, que no caso ideal podem ser somente uma única vibração. Esta vibração é sempre transversal ao sentido do curso do feixe.
O polarizador é apenas um seletor. Não cria vibrações transversais, mas seleciona preferencialmente determinadas vibrações transversais e rejeita todas as demais. Esta seleção é realizada usando um ou vários dos princípios de absorção, de reflexão, e de refração. Aqui o poremos a par com os tipos correntes de polarizadores, como trabalham, e como usá-los.
Para compreender melhor este módulo, você deve compreender a teoria da luz polarizada.
Este artigo complementa a Base Geral da Terminologia Óptica 5 referente aos filtros. Vamos tentar demonstrar virtualmente todas as propriedades conhecidas na polarização para o conhecimento da maioria dos interessados na questão.
Vamos explicar as definições e diferenças entre:
- Onda transversal
- Polarização plana
- Polarização vertical
- Polarização circular e elíptica
- Polarizador Dicróico
- Polarizador da reflexão
- Polarizador do Dupla-refração
- Placa de Quarto de onda
- Placa de Meia onda
Conhecerá os diversos tipos de polarizadores:
- Polarizador H-Polaroid
- Polarizadores de Película fina
- Polarizador de Glan-Foucault
- Polarizador de Glan-Thompson
- Polarizador de Nicol
- Polarizador de prisma de Rochon
- Polarizador de prisma de Wollaston
Conhecerá também:
- O que é ângulo de Brewster para placas lisas em vários meios.
- Os diversos usos práticos dos polarizadores,
- A lei de Malus.
DISCUSSÃO
A luz é uma forma de movimento de onda, que viaja rapidamente no espaço (300.000 km – ou 186.326 milhas por segundo) não podemos ver como as ondas vibram. Porém, os movimentos das ondas devem ser conhecidos para que possamos descrever o funcionamento dos polarizadores. Assim, descreveremos algumas características importantes das ondas em geral.
Mesmo sem pudermos vê-las, experiências demonstram que os campos elétricos e magnéticos presentes nas ondas vibram perpendicularmente ao sentido do curso do feixe. A luz conseqüentemente é constituída de ondas transversais. Por exemplo, se o sentido do curso de um feixe luminoso dado está do leste, as vibrações elétricas podem estar para cima e para baixo, ou Norte e Sul, ou ao longo de toda a outra linha perpendicular à linha central leste-oeste.
A Figura a seguir mostra um "instantâneo" de uma onda plano-polarizada que viaja da esquerda para a direita, composta de componentes elétricos (vetor E) e de componentes magnéticos transversais (vetor B).
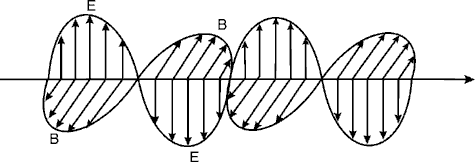
Fig. 1
Instantâneo da onda plana de luz polarizada
O plano que contem o vetor E e o sentido da propagação é chamado de plano de polarização. Na figura 1 é mostrado como o plano vertical. No trabalho da polarização, o sentido do vetor E é especificado, assim, apenas o componente elétrico será e considerado durante o restante deste módulo. Na onda transversal plano-polarizada é necessário especificar os dois sentidos: aquele do distúrbio de onda (o vetor E) e aquele da propagação. Em ondas transversais plano-polarizadas, nós podemos assim esperar uma falta da simetria sobre a linha central da propagação. Esta falta da simetria no limite é a polarização, mas vamos ainda estabelecer essa definição com mais clareza.
As ondas eletromagnéticas no rádio e nas microondas exibem imediatamente esta falta da simetria. Estas ondas, geradas pela variação da carga acima e abaixo do dipolo que forma a antena transmissora, tem um vetor de campo elétrico paralelo à linha central do dipolo. Isto é demonstrado na figura seguinte.
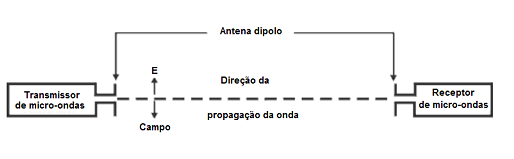
Fig. 2
Geração do campo E nas microondas
Quando esta onda plano-polarizada cai em um segundo dipolo conectado a um detector de microonda, o componente elétrico de alternância da onda fará com que os elétrons afluam para frente e para trás na antena de recepção, produzindo uma indicação no detector. Se nós giramos a antena de recepção com 90° em relação ao sentido da propagação? -A leitura do detector cairá a quase zero. Nesta orientação o vetor de campo elétrico não pode fazer com que a carga se mova ao longo da linha central do dipolo porque neste caso, a antena aponta perpendicularmente para a linha central.
A maioria de fontes de luz visível difere das fontes de microondas mostradas acima. Pois os irradiadores elementares -isto é, os átomos e moléculas -atuam totalmente independentes. A luz propagada em um dado sentido consiste em trem de ondas independentes cujos planos de vibração são orientados aleatoriamente sobre o sentido da propagação. Esta situação é mostrada em figura 3 na qual se vê a onda pelo seu eixo ao longo do sentido da propagação (para o papel).
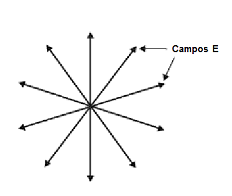
Fig. 3
Luz não polarizada
Este eixo de luz, embora apesar de transversal, é não polarizada. A finalidade principal dos polarizadores é selecionar os diferentes planos de vibração de uma radiação. A luz polarizada é a luz cuja vibração transversal tem uma formatação padrão simples. A figura 4 mostra uma onda de luz que viaja ao longo do eixo Z de um sistema coordenado pela mão direita. As vibrações elétricas são horizontais e, portanto a luz é dita como polarizada linear e horizontalmente.
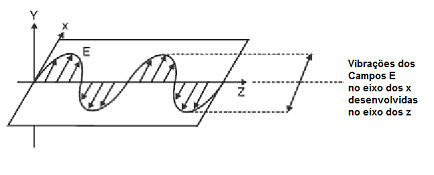
Fig. 4
Luz linearmente polarizada, horizontalmente, no
plano X-Z
A porção direita da figura 4 mostra a forma da seção, que corresponde a uma fotografia de um determinado momento tomado por uma câmera que olha pela seção transversal do feixe. A câmera é situada na linha central do feixe e apontada em linha reta na fonte luminosa. Quando as vibrações transversais são verticais, a seção transversal do movimento da onda está indicada por uma linha vertical, e a luz é polarizada linear e verticalmente. Este caso é mostrado em figura 5.
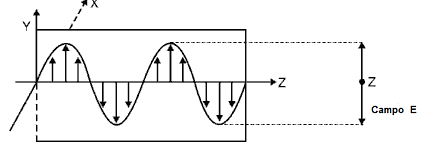
Fig. 5
Luz linearmente polarizada, verticalmente,
no plano
Y-Z
Não pressuponha pela figura que a luz “espirre” pelos lados. O desenho deve ser interpretado como uma forma da força do campo elétrico dentro da onda de luz em função da distância, ou do tempo, percorridos.
Com o relacionamento apropriado das fases entre os feixes polarizados vertical e horizontalmente, o instantâneo da forma é uma hélice e a formatação secional é um círculo. Este caso é mostrado em figura 6.
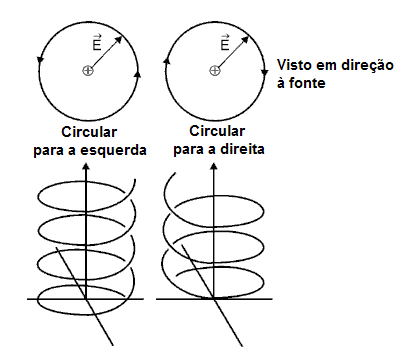
Fig. 6
Formação da luz de polarização circular
Pela convenção a mais comum, se a luz é vista olhando-se em direção a fonte e o campo elétrico gira no sentido horário, a polarização é chamada circular para a direita; Similarmente, uma rotação no sentido anti-horário seria chamada circular para a esquerda ou polarização trigonométrica.
A figura 7 mostra como duas ondas plano-polarizadas de igual amplitude e perpendicularmente entre si podem criar a luz circular polarizada. E se as duas ondas de figura 7 diferirem em fase por 90°? Neste caso onde uma onda tem valores máximos, a outra terá zero. Os valores das amplitudes resultantes das duas ondas para as posições 1 a 8, serão vistas por um observador que olha para a onda que se aproxima, são indicados nos pequenos quadrados sob o desenho da onda. Note que um observador que olha para a onda se aproximando verá o vetor resultante girar no sentido anti-horário com tempo e forma gerando a luz polarizada circular da mão esquerda.
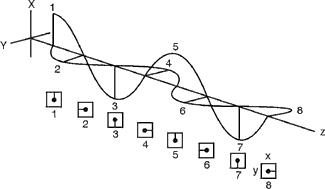
Fig. 7
Formação da luz de polarização circular.
Para clareza, apenas os vetores de campos elétricos são mostrados.
De maneira similar, se as amplitudes dos componentes horizontais e verticais do campo elétrico não são iguais, teremos a produção de uma luz polarizada elíptica. Como uma alternativa, a diferença de fase entre os componentes pode ser mudada para produzir a polarização elíptica. Você pode encontrar uma completa discussão de tais efeitos nos textos de física sob o tópico de figuras de Lissajous.
Os polarizadores são dispositivos que mudam a luz do estado não polarizado demonstrado na figura 3 a um ou vários estados mostrados pelas figura 4, 5, e 6. O restante deste módulo será dedicado como os polarizadores operam e como são usados.
Tipos de Polarizadores
No laboratório o método usual de produzir a luz polarizada é o método dos três passos primeiramente produz-se uma luz não polarizada comum, então se reduz esta luz a dois componentes ortogonais polarizados, e finalmente eliminamos um destes componentes. O componente que permanece é luz polarizada. Este processo é ineficiente, mas barato e simples.
Um polarizador é na realidade um divisor-e-seletor. Não cria vibrações transversais. Divide apenas as vibrações existentes em duas classes. Há muitos tipos de polarizadores. Isso é porque muitos tipos de manipulações óticas podem ser usados. Os processos de absorção, de reflexão, de refração, e de dispersão podem ser usados para dividir um feixe em componentes polarizados.
Polarizadores Dicróicos
Os materiais Dicróicos têm a propriedade de seletivamente absorverem um dos dois componentes ortogonais da luz comum. O dicroísmo é exibido por uma série de minerais e por alguns compostos orgânicos.
O dicroísmo foi descoberto no início do século XIX. Um dos cristais que exibem a propriedade é a, turmalina, foi um polarizador de uso geral durante muito tempo. Embora este cristal em particular tivesse muitas deficiências, o mesmo princípio de dicroísmo foi usado para produzir o polarizador mais comumente usado, as laminas tipo-H da Polaroid.
A analogia a mais simples a um polarizador dicróico é dada pela grade de fios mostrada na figura 8. Podemos explicar a teoria dicróica do polarizador simplesmente nos termos deste dispositivo. O polarizador de grade de fios consiste numa disposição fios delgados paralelos um ao outro. Os fios de metal fornecem alta condutividade para os campos elétricos paralelos aos fios. Tais campos produzem correntes elétricas nos fios, como na antena de receptor do tipo dipolo nas microondas. A energia dos campos é convertida em energia de corrente elétrica nos fios. Esta corrente é convertida então em calor por causa da pequena, mas significativa resistência elétrica dos fios.
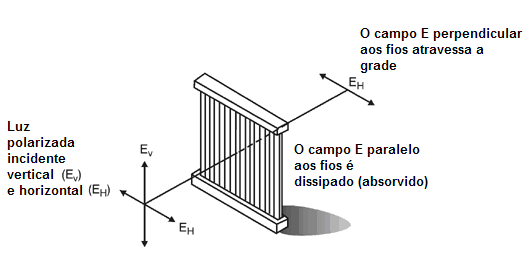
Fig. 8
Polarizador de grade de fios
Por causa dos espaços não condutores entre os fios, nenhuma corrente pode fluir perpendicularmente. Os campos elétricos perpendiculares aos fios não produzem virtualmente nenhuma corrente e perdem pouca energia. A grade de fios, quando colocada em um feixe não polarizado, drena apenas a energia de um componente e deixa os outros passarem sem nenhuma atenuação. O componente transmitido é aquele em que o campo elétrico vibra numa perpendicular ao sentido dos fios.
Um exemplo de luz que passa através de um material dicróico é mostrado na figura 9. A luz aleatoriamente polarizada que entra em T1 é reduzida à uma simples polarização vertical, que passa por T2 sem ser afetada enquanto sua orientação é a mesma de T1. E se o T2 for girado em 90°? -Terá o efeito de dois polarizadores de grade de fios perpendiculares entre si, e virtualmente não haverá nenhuma passagem de luz.
Apesar do polarizador de grade de fios ser de fácil compreensão, o mesmo é extremamente difícil de ser executado. Os fios deverão estr afastados apenas de um comprimento de onda entre si e isto é impossível de ser manipulado.
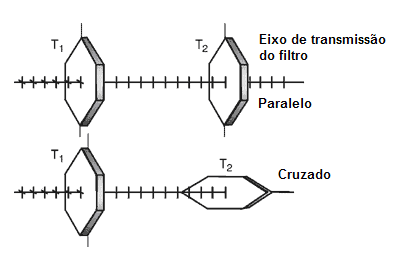
Fig. 9
Como opera um polarizador dicróico
Uma maneira melhor deveria ser encontrada. Isto aconteceu em 1938 em que O Dr. E.H. Land inventou a lâmina H-Polaroid. Veja a lâmina H-Polaroid como uma versão química da grade de fios. Em vez dos fios finos e longos, a lâmina H-Polaroid utiliza as finas e longas moléculas do álcool de polivinil que contêm muitos átomos do iodo. Estas moléculas longas, e retas estão quase perfeitamente paralelas se alinhado umas às outras a aproximadamente 3 Šapart. Por causa da condutibilidade oferecida pelos átomos do iodo, o componente elétrico da vibração paralelo às moléculas é absorvido. O componente perpendicular às moléculas passa completamente e com pouca absorção.
A forma com que Land produziu este tipo de polarizador é mostrada na figura 10. Uma folha de álcool de polivinil é aquecida e então esticada (laminada, estirada) rapidamente a muitas vezes seu comprimento. Durante a operação de estiramento as moléculas longas do polímero são giradas mais para que tenham quase o mesmo sentido, a saber, o sentido da força de estiramento.
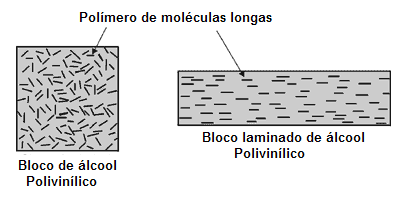
Fig. 10
Produzindo um filtro H-Polaroid
A etapa seguinte foi mergulhar esta folha esticada numa solução líquida rica em iodo. Os átomos do iodo difundem na camada do álcool polivinilico e unem-se às moléculas finas, quase paralelas. Assim os átomos do iodo imitam seu hospedeiro tomando a forma de correntes finas longas.
Estas correntes de iodo na folha Polaroid atuam como fios. Absorvem as vibrações do campo elétrico paralelas a sua linha central e transmitem livremente as vibrações perpendiculares a essa linha central. Assim a linha central da transmissão é perpendicular ao sentido esticado.
A figura 11 mostra o efeito do material Polaroid na luz quando duas folhas são alinhadas paralelamente e quando as duas são perpendicularmente usadas.
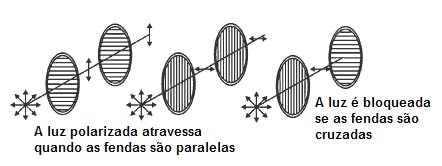
Fig. 11
Efeito de materiais polarizados na luz
Muitos outros tipos de polarizadores dicróicos laminados podem ser feitos. Algumas usam tinturas que consistem em moléculas finas longas, e algumas usam cristais finos longos. Entretanto, todos estes tipos são similares na teoria às folhas do tipo Polaroid aqui mencionadas.
Polarizações TM e TE
Antes de continuarmos nosso exame dos métodos de polarização da luz, será útil definir dois tipos particulares de polarizações, o TM (magnético transversal) e o TE (elétrico transversal). Estas duas polarizações ortogonais (mutuamente perpendiculares) são mostradas em figura 12. Observe que as setas curtas (polarização TM) na figura 12a representam um campo elétrico que vibra no plano da página, perpendicular ao sentido do feixe. Os pontos (polarização TE) na figura 12b representam um campo elétrico que vibra para dentro e para fora, perpendicular ao plano da página. Estas vibrações são também perpendiculares ao sentido do feixe.
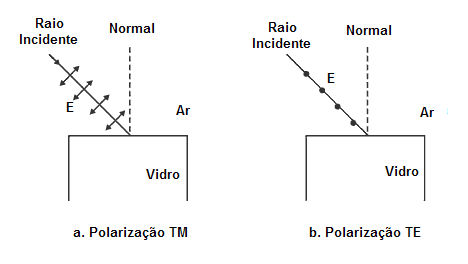
Fig. 12
Duas polarizações ortogonais da luz
Os vetores TM e TE são definidos no que diz respeito ao assim chamado; "plano de incidência" (POI) que é o plano que contém a normal à superfície e ao raio de incidência. Assim na figura 12, a POI é o plano da página. Observe que na figura 12a o campo elétrico está contido em POI. Isto significa que o campo magnético deve ser transversal (através ou perpendicular) ao plano POI. Por outro lado, a figura 12b mostra a polarização TE com o campo elétrico transversal (perpendicular) à POI. Em ambas figuras para as polarizações TM e TE, apenas o campo elétrico é mostrado para evitar confusão visual.
Polarizadores do tipo Refletivos
Talvez o método mais simples de polarização da luz foi o descoberto por Malus em 1808. Se um feixe da luz branca não polarizada incide em um determinado ângulo em uma superfície polida de uma placa do vidro comum, este se encontra em polarização linear devido à própria reflexão.
Quando a placa de vidro está orientada para ser perpendicular ao feixe (fazendo zero graus com a normal) nenhuma polarização da luz existes. Todos os componentes da vibração da luz são transmitidos igualmente e o feixe transmitido não é polarizado. Aproximadamente 8% é refletido, (4% na superfície superior) e a luz refletida é igualmente não polarizada.
Quando o raio incidente é inclinado de forma a criar um ângulo q com a normal, a simetria do processo de reflexão é destruída, e os raios transmitidos e refletidos encontram-se parcialmente polarizados. Esta situação é mostrada na figura 13a.
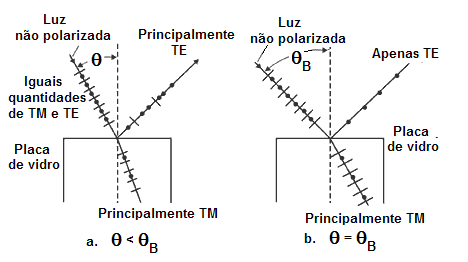
Fig. 13
Reflexões de polarizações TM e TE em uma superfície plana
Quando o ângulo de incidência é aumentado para o chamado ângulo de Brewster qB, a polarização TM é 100% transmitida, o que deixa o feixe refletido como pura polarização TE, segundo demonstrado na figura 13b. Veja, porém que parte da polarização TE está ainda presente no feixe transmitido, mas nenhuma polarização TM está presente na parcela refletida do feixe de incidente. Você pode encontrar o ângulo de Brewster da expressão:
|
|
Equação 1 |
|
onde: |
n2 |
= |
Índice de refração da placa de vidro |
|
n1 |
= |
Índice de refração do meio próximo ao vidro |
Por exemplo, para uma placa de vidro (n2 = 1.52) no ar (n2 = 1.00), A equação 1 será:
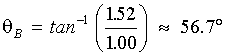
Se você estudou a introdução aos lasers, você recordará que este é o ângulo no qual a janela Brewster orienta o laser para a extremidade de um tubo de plasma. Isto é comum, por exemplo, em a maioria de lasers de íon de argônio ou do criptônio.
Às vezes os polarizadores de placa de reflexão são compostos de diversas placas e são chamados de polarizadores de "placas empilhadas"; ou " Brewster Stack". Usando-se muitas placas aumentamos pureza da polarização transmitida removendo-se assim cada vez mais a polarização TE. As pilhas de Brewster são geralmente de dois tipos -lineares ou angulados. O último tem a vantagem de produzir um feixe coincidente com a fonte original. (Veja figura 14.)
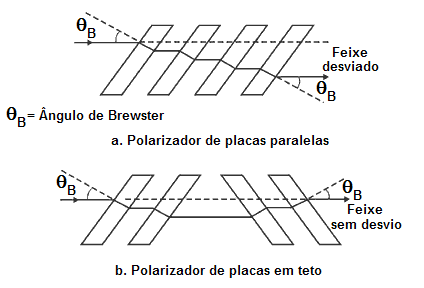
Fig. 14
Tipos de polarizadores de placas empilhadas
Os polarizadores do tipo de reflexão têm diversas características atrativas. Podem ser projetados para o uso em qualquer parte do espectro. Também, são fáceis de fazer e possuem elevada resistência aos danos causados pelo laser. Porém os polarizadores do tipo reflexão raramente são usados para polarizar a luz na região visível porque eles são superados pelos polarizadores de lâmina discutidos previamente. Somente em determinadas regiões da escala infravermelha e ultravioleta os tipos de reflexão são superiores, ou em aplicações de laser de alta potência onde outros tipos de polarizadores sofreriam danos imediatos.
Outros tipos de polarizadores baseados na reflexão (e na transmissão) estão igualmente se tornando importantes em aplicações de laser de elevada potência. Estes polarizadores são constituídos geralmente sob a forma de revestimentos dielétricos finos. São chamados assim de "polarizadores de película fina". Há dois tipos principais:
O primeiro polarizador de película fina, chamado de polarizador biprisma de MacNielle, usa um dielétrico multicamada de película fina entre dois prismas. O segundo é mais usado geralmente por causa de seu custo e possibilidade de ser construído em tamanhos maiores. É a pilha multicamada de película fina que substitui apropriadamente o biprisma de MacNielle. Esta combinação é usada então em um ângulo apropriado no feixe.
Simplesmente dizendo, estes polarizadores, similares em várias formas aos filtros de película fina, possuem grandes diferenças nas características de reflexão e de transmissão para os dois tipos de polarização, TM e TE, em um comprimento de onda selecionado específico. A relação entre a transmissão das polarizações TM e TE chamada às vezes de “relação de extinção” - pode alcançar várias centenas ou até mil.
Uma discriminação aumentada pode ser conseguida usando-se diversas placas combinadas. Entretanto, estes polarizadores de película fina são razoavelmente sensíveis à orientação angular. Para uma descrição mais completa destes novos polarizadores, veja o artigo escrito por Austin.
Polarizadores de Dupla-refração
A polarização foi descoberta com o auxílio de cristais que exibem o fenômeno da dupla refração. Foi descoberta pelo cientista holandês Huygens quando estudava alguns cristais de calcita, mineral de dupla refração (CaCO3). A dupla refração é um assunto complexo que exige uma exata compreensão de cristalografia. Devido à complexidade da estrutura do cristal, não explicaremos as razões da dupla refração. Vamos nos concentrar no efeito da calcita no feixe luminoso.
Se um cristal de calcita polido é colocado sobre um ponto preto, a imagem do ponto aparece duas vezes. Esta dupla dobra de um feixe luminoso através da calcita é chamada de dupla refração. A figura 15 mostra um feixe da luz não polarizada que incide em um cristal da calcita. O sentido da simetria através do cristal -conhecido como eixo óptico- funciona diagonalmente ao longo do cristal, de A para B. Com o eixo óptico neste sentido, um único feixe se divide em dois na superfície de cristal.
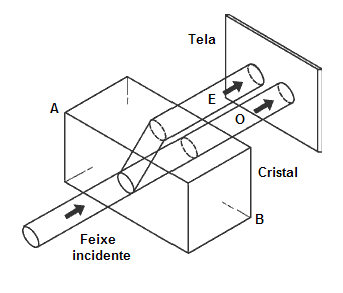
Fig. 15
Dupla refração da luz não polarizada. A direção do eixo
óptico no cristal (não representado) é diagonal de A para B.
Se você experimenta em vários ângulos de incidência, você encontrará que um dos feixes de figura 15 obedece a lei de refração de Snell na superfície de cristal (veja nossa base Geral da Terminologia óptica parte 2), da mesma forma como todo o raio luminoso que passa de um meio a outro. Este feixe é dado como "ordinário" ou raio O na figura 15.
O outro feixe refratado não obedece às leis de refração. Este feixe é chamado de "extraordinário" ou raio E. Você compreenderá a diferença entre as ondas representadas pelos raios E no que diz respeito às leis de refração nestes termos:
- A onda O viaja no cristal com a mesma velocidade Vo, em todas as direções. Ou seja o cristal tem, para esta onda, um único índice de refração, no, exatamente como um sólido isotropic.
- A onda E viaja no cristal com uma velocidade que varia
em cada ua das direções. Na calcita varia do
Vo a um
valor maior Ve. Os raios E e O da
figura 15 são polarizados perpendicularmente entre si e são ~ 100% polarizados.
Simplesmente falando, um cristal de dupla refração divide a luz em dois componentes fazendo com que um tipo de vibração viaje por um trajeto enquanto o outro tipo viaje por um outro trajeto. Em todos os casos, é importante saber os sentidos relativos do eixo óptico e do sentido da vibração da luz de incidente. O eixo óptico é o sentido de um cristal em torno do qual todos os átomos estão simetricamente dispostos. Assim se você olha ao longo do eixo óptico de um cristal, você "vê " - como um fóton caminha- a mesma disposição dos átomos acima, abaixo, à direita e à esquerda desta linha central. A luz ao longo deste sentido tem uma velocidade diferente de viajando perpendicularmente a este sentido. Assim teremos eixos (caminhos) rápidos e lentos a partir das faces do cristal.
Deve estar claro que construir um polarizador de calcita é fácil. De fato todo o cristal de calcita de face lisa já é um polarizador. A estrutura natural de cristais de dupla refração faz com que polarizem a luz, pois Quando a luz viaja dentro do cristal em sentidos ligeiramente diferentes, dependendo de sua polarização, as polarizações emergem em lugares ligeiramente diferentes. Assim constituem dois feixes lado a lado de luz linear polarizada com sentidos de vibração mutuamente perpendiculares. A menos que o feixe incidente seja muito delgado ou o cristal muito grande, os dois feixes emergentes vão se sobrepor parcialmente. Diversas formas geométricas foram dadas à calcita que superam este problema.
O Polarizador de Glan-Foucault
Um projeto de um polarizador de calcita foi inventado por Glan e por Foucault. É mostrado na figura 16. São usadas duas partes triangulo-retangulares de calcita. As duas partes são montadas lado a lado e seguras de modo a haver uma estreita abertura de ar entre as hipotenusas respectivas segundo as indicações de figura 16.
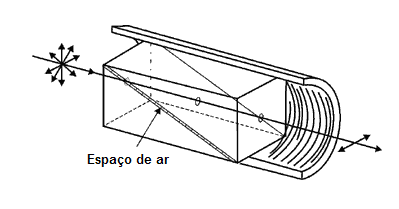
Fig. 16
Polarizador de Glan
Quando um feixe da luz não polarizada incide num prisma ao longo da normal à face de saída, ele entra no prisma e forma dois feixes, a saber: o raio O e o raio E. Os inventores escolheram um ângulo para a hipotenusa de modo que um feixe seja internamente totalmente refletido e que o outro seja transmitido. Isto é mostrado em figura 17.
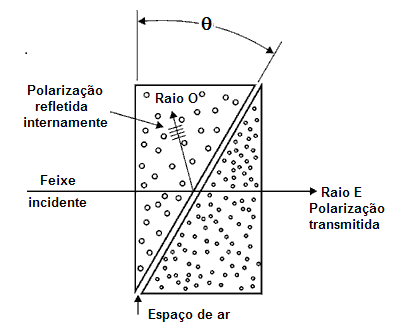
Fig. 17
Como funciona o polarizador de Glan
O feixe refletido que incide sobre a parte preta no lado do primeiro prisma é absorvida. O feixe transmitido prossegue adiante, pela abertura de ar, e através do segundo prisma. O grau de polarização deste feixe é praticamente 100%.
Pelo fato da calcita ser transparente do ultravioleta (230 nanômetros) ao infravermelho (5000 nanômetros), e porque o polarizador de Glan ser apenas constituído de calcita, este polarizador pode ser usado em toda a larga faixa espectral. Um inconveniente, entretanto, é que o feixe incidente deve atingir a face de entrada em ângulo não maior de 7° com a normal.
O Polarizador de Glan-Thompson
Se os dois prismas do polarizador de Glan-Foucault estão colados entre si e a abertura de ar eliminada, o dispositivo será chamado de polarizador de Glan-Thompson. Tem uma vantagem sobre o polarizador de Glan-Foucault pois pode aceitar a luz de incidente superior ao ângulo de 7°. Um inconveniente deste tipo é que o cimento usado é normalmente opaco a determinados comprimentos de onda e pode ser danificado em intensidades de luz elevadas.
O Polarizador de Nicol
Um outro dispositivo de polarização muito útil feito da calcita é o polarizador de Nicol. O polarizador de Nicol, como os polarizadores de Glan, remove um dos raios refratados através da reflexão total que se realiza dentro do polarizador. Como vemos na figura 18, o polarizador de Nicol é feito igualmente de duas cunhas triangulares de calcita. Neste caso, as cunhas são cimentadas bálsamo de Canadá que tem um índice de refração intermediário entre os índices dos raios O e E. O ângulo de tolerância que o raio de luz incidente pode entrar em um polarizador de Nicol mantendo com sucesso sua função é de aproximadamente 14°.
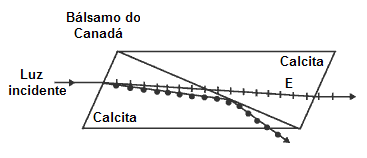
Fig. 18
Polarizador de Nicol
O polarizador de Nicol é eficiente. Mas tem uma escala espectral limitada por causa da absorção da luz ultravioleta causada pelo bálsamo de Canadá.
Separador Cúbico de Rochon e Polarizadores de Wollaston
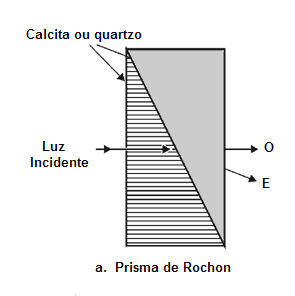
Os tipos de polarizadores de dupla refração mencionados acima são projetados para transmitir um dos feixes e absorver o outro. Às vezes você precisa de um dispositivo de polarização que transmita ambos os feixes e os separe o bastante de modo que cada feixe possa ser usado independente. Este dispositivo servirá então como um polarizador e um divisor de feixe de polarização. Isto acontece no prisma de Rochon demonstrado na figura 19a.
|
|
|
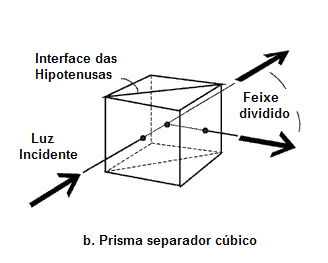
Fig. 19
Prisma de Rochon e o prisma separador cúbico
Na primeira metade do prisma de Rochon, os cursos dos raios ordinários e extraordinários seguem com a mesma velocidade. Na segunda metade, o raio ordinário continua na mesma velocidade. Mas o raio extraordinário viaja mais rapidamente e conseqüentemente é desviado por um valor que depende do ângulo na face de entrada.
O separador cúbico mostrado na figura 19b consegue uma separação dos feixes polarizados, da ordem de 90°, maior do que com o prisma de Rochon. Os separadores cúbicos são feitos cimentando dois prismas de precisão em ângulo reto. Antes de cimentar, uma película do metal-dielétrico é depositada a vácuo em uma das faces das hipotenusas. Este separador cúbico, disponível nas dimensões de 5 mm a 50 mm de arestas, estão mecanicamente rígidos e livres de imagens fantasma. Revestimentos anti-reflexo de uma só camada de Mg F2 são aplicados às faces da entrada e da saída do prisma de vidro tipo BK-7.
O polarizador de Wollaston mostrado na figura 20 comporta-se de maneira similar. Mas este desvia os feixes em direções opostas. O raio ordinário na primeira metade do prisma se transforma no raio extraordinário na segunda metade, e vice versa. Assim um raio é desviado pelo mesmo valor que um prisma de Rochon desviaria o raio extraordinário, e o outro também é desviado praticamente pelo mesmo valor.
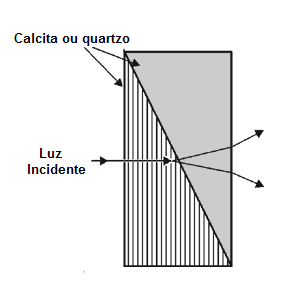
Fig. 20
Prisma de Wollaston
O prisma de Rochon é usado em instrumentos óticos para produzir um feixe plano-polarizado. O feixe O é usado e o feixe E é projetado para fora em uma distância suficientemente grande do prisma.
O prisma de Wollaston é usado onde uma comparação de intensidades é desejada. Ambos os feixes são usados. As intensidades dos dois feixes serão iguais se o feixe da entrada não for polarizado, mas diferirão se o feixe da entrada for minimamente polarizado.
Retardadores-Conversores de Polarização (Placas de Onda)
Os retardadores não são polarizadores no sentido estrito da palavra. Não têm nenhum efeito na luz não polarizada. Mas são muito úteis em mudar a orientação ou a forma da luz polarizada. No uso comum, as palavras "retardador" e "placas de onda"; referem-se ao mesmo dispositivo.
O princípio de operação de um retardador ou de uma placa de onda é facilmente definido. – Divide o feixe polarizado incidente em dois componentes, mudam as fases relativas entre os dois raios (O e E), enquanto passam através da placa da onda e os recombina na saída da placa de onda. Por causa do deslocamento da fase resultante, a luz que sai do sistema tem diferentes propriedades de polarização. Desde que a etapa chave é a introdução de um deslocamento de fase relativo, alguns chamam este mesmo dispositivo de "deslocador da fase", "placa de onda", ou "retardador".
Um retardador típico consiste em uma placa cristalina fina segundo as indicações de figura 21. Suponhamos que um feixe linearmente polarizado seja incidente na placa pela esquerda como mostrado. Você pode considerar que o feixe incidente possua vibrações nos planos vertical e horizontal. O fato importante é que as duas vibrações na placa de onda viajarão em velocidades diferentes de modo que, quando emergem, uma foi retardada ou defasada se comparada à outra.
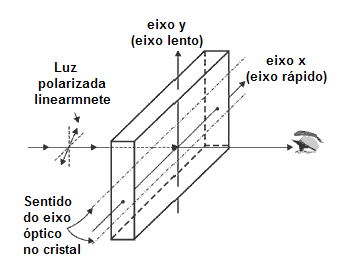
Fig. 21
Retardador 180°
Nós estamos interessados somente no atraso relativo. Na calcita o feixe com a vibração vertical é retardado. Este sentido vertical é chamado de "eixo lento". O sentido em que a vibração do feixe viaja mais rápida é inversamente chamado de "eixo rápido".
A espessura da placa da onda assim como o tempo que a luz gasta no interior do cristal determina a quantidade de deslocamento de fase. Se o deslocamento de fase é 90°, o retardador é uma placa de um quarto de onda. Pode converter a luz polarizada linearmente em luz polarizada circularmente, e vice-versa. Uma placa de meia onda gira o plano incidente de polarização num ângulo de 2q, onde q é o ângulo que o sentido de vibração da luz incidente polarizada faz com o sentido do eixo óptico na face do cristal. A figura 22 mostra os efeitos de uma placa de um quarto de onda e de uma placa de meia onda.
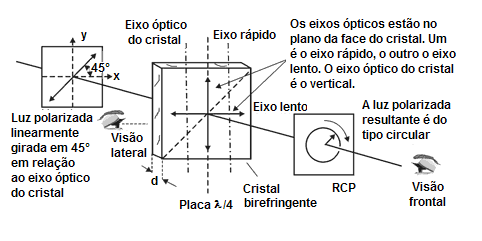
(a) A placa de um quarto de onda converte a luz linearmente polarizada em circularmente polarizada.
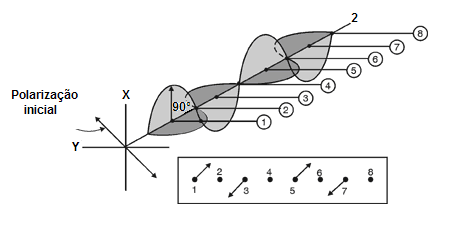
(b) Desenvolvimento da luz circularmente polarizada por uma placa de um quarto de onda.
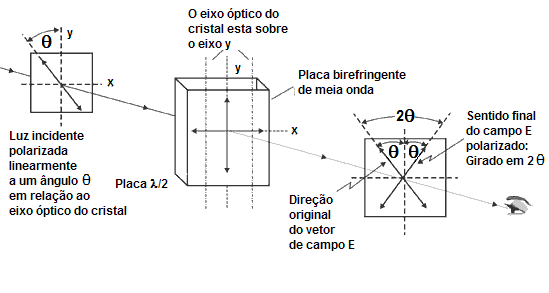
(c) Placas de meia onda giram a luz linearmente polarizada num ângulo 2q em relação ao eixo óptico do cristal.
Fig. 22
Uma placa de meia onda gira a luz linear (l/2)
Na figura 22a, a luz linear polarizada, orientada em 45° na direção do eixo óptico do cristal, é tratada como componente x e componente y, cada um igual ao outro. Ao entrar num cristal birefringente, o componente y, alinhado com o eixo rápido, viaja com o mais depressa do que o componente x, que se alinha com o eixo lento. Os dois componentes são então defasados em 90° entre si, tal que ao emergirem, um é sempre máximo enquanto o outro será sempre zero e vice versa. (Veja a figura 22b).
O efeito é produzir a luz polarizada circular, como visto por um observador que olha para dentro do cristal. O deslocamento de fase de 90° é produzido por uma espessura d exata do cristal birefringente, que, por causa do deslocamento de 90°, é referido como uma placa l/4.
A figura 22c mostra como uma placa de meia onda (l/2) gira a luz linearmente polarizada, inicialmente orientada num ângulo q com o eixo óptico do cristal para um ângulo de 2q. A luz linearmente polarizada mostra, portanto um ângulo q no lado oposto do sentido do eixo do cristal.
Note que a espessura real da placa de l/4 ou l/2 não é igual a l/4 ou l/2! (isto faria certamente desta uma placa extremamente FINA!) Os símbolos l/4 ou l/2 referem-se simplesmente ao efeito de separar os dois componentes -RÁPIDOS e LENTOS por 90° (l/4) ou 180° (l/2). A verdadeira espessura da placa de onda -depende do deslocamento de fase desejado, do comprimento de onda no vácuo da luz incidente e dois índices de refração dos componentes da onda que viajam ao longo do eixo rápido e do eixo lento do cristal.
Usos dos Polarizadores
Os polarizadores são usados em nossas vidas quotidianas assim como no laboratório de óptica. Aqui daremos alguns exemplos de usos populares.
Os óculos de sol de polarização aproveitam-se do fato que o brilho natural dos objetos consiste principalmente na vibração da luz em sentido horizontal. A razão para isto é que a luz solar vem de cima para baixo e incide na maior parte das vezes em superfícies horizontais (tais como os oceanos). Os reflexos de tais superfícies conduzem à polarização da luz com uma predominante vibração horizontal. (Veja a figura 13a.) A figura 23 mostra que em óculos de sol de polarização a linha central da transmissão é vertical e reduz assim o brilho refletido das superfícies horizontais.
Fig. 23
Óculos de sol Polarizadores
Este mesmo princípio é utilizado na fotografia, de uma maneira mais complexa e abrangente. Neste caso, objetos são registrados e os objetos possuem formas variadas, portanto reflexos podem provir de varias posições e de vários planos. Por isto usa-se o filtro polarizador à frente da objetiva da câmara fotográfica. Neste caso usam-se filtros polarizadores do tipo plano (linear) ou do tipo circular, que na fotografia final tem o mesmo efeito, mas que alteram os sensores das várias câmaras fotográficas conforme o seu tipo. Os filtros possuem um anel frouxo para que o operador o coloque visualmente na posição que melhor lhe aprouver.
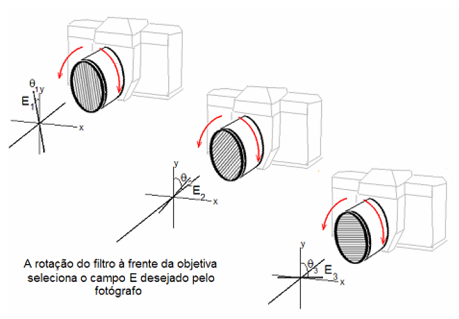
Fig. 24
Filtros Polarizadores
Em uso prático, os polarizadores circulares, atualmente tão discutidos, em nada diferem dos polarizadores lineares, a não ser pela razão acima explicada, de não confundir os sensores dos aparelhos de nova geração. V. terá em mente, porém que, enquanto os polarizadores lineares, ao selecionarem o plano E de vibração este chegará até o plano do filme ou sensor de forma imutável, isto é, sempre no plano E, o polarizador circular selecionará o Vetor E que atinge a primeira superfície do polarizador e colocará o vetor após emergir deste filtro em movimento espiral (para esquerda ou direita de acordo a natureza da fonte) até atingir o plano do filme ou sensor digital da câmara em questão. (Verifique as figuras 6 e 7 para visualização do fenômeno) Aqui V. já deve ter percebido a sutileza: A Polarização circular é dependente do foco da objetiva. Isto é: Se a objetiva estiver mais para trás ou mais para frente, o efeito final de polarização será diferenciado. Portanto, o filtro deverá sempre ser reajustado após a focalização. Apesar de parecer um pouco mais complicado, este sistema só se usa em câmaras de foco automático, o que dispensa a atenção do operador.
As soluções de vários açúcares e de outras substâncias orgânicas têm a propriedade de girar o plano de polarização da luz que passa através deles. A extensão desta rotação é medida com um polarímetro. Segundo as indicações de figura 24, este instrumento é constituído de uma fonte de luz (geralmente uma lâmpada do sódio), de um polarizador, um tubo para prender a amostra e um analisador. Um analisador é um simplesmente outro polarizador que possa ser girado.
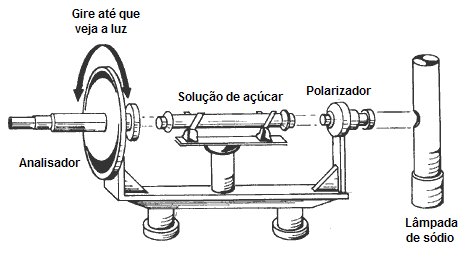
Fig. 25
Polarímetro
Para usar o dispositivo, o tubo primeiramente é cheio com água destilada, a lâmpada é ligada, e o analisador girado até que nenhuma luz seja vista. O polarizador e o analisador estão então "cruzados". A água no tubo é substituída então pela solução sob teste. O analisador é girado outra vez até que esteja cruzado outra vez com o polarizador. A mudança no plano de polarização é determinada assim. Tal informação fornece indícios à estrutura destes compostos. A quantidade e o sentido da polarização indicam a força, a concentração, e o tipo da solução.
Um outro exemplo do uso da polarização é a célula de Kerr que foi usada na fotografia de alta velocidade e em feixes de luz de modulação. Vamos abaixo demonstrar esta curiosa utilização com mais detalhes. Esta célula pilha depende dos efeitos de polarização induzidos em um líquido segundo as indicações de figura 25.
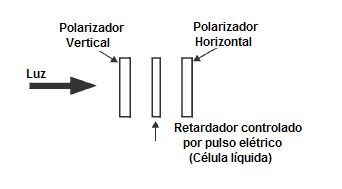
Fig. 26
Célula de Kerr
A luz é polarizada verticalmente pelo primeiro polarizador e, a menos que seja mudada em 90° no retardador, não poderá passar no segundo polarizador orientado horizontalmente. Este arranjo forma um obturador que possa abrir e se fechar em 10–12 segundos. Um efeito similar ocorre em alguns materiais sólidos e é chamado de "Efeito Pockels". As células de Pockels são usadas, por exemplo, como interruptores Q para laser e praticamente substituíram as volumosas células de Kerr.
A meu ver em particular o emprego visualmente mais espetacular da polarização foi o da Vectografía. Que consiste na superposição de duas placas tipo H-Polaroid ambas com com o registro da imagem olho direito/olho esquerdo e orientadas a 45° com o eixo vertical e a 90° entre si. O processo também desenvolvido pelo Dr. Land, foi bem aplicado na 2ª Guerra Mundial para o aprendizado de motores aos futuros mecânicos sem necessidade vê ter que vê-los pessoalmente. Uma fotografia de grandes dimensões era então visualizada diretamente em 3D através de óculos polarizadores.
Na impressão Vectográfica a própria imagem é um polarizador. Da mesma forma que os demais polarizadores ela transmite livremente apenas um componente da luz. Contudo, enquanto um polarizador comum absorve virtualmente todos os demais componentes, na Vectografía a imagem absorve este componente apenas na proporção de sua densidade. Assim, todos os componentes serão absorvidos em área de alta densidade, e muito pouco nas áreas de baixa densidade (transparentes).
Quando a imagem é visualizada através de um polarizador paralelo a sua orientação a imagem Vectográfica torna-se invisível. Se através de um polarizador a 90° de seu eixo, a imagem é vista em sua plenitude de contraste.
Se duas imagens Vectográficas são superpostas com seus eixos a 90° entre si, (em sanduíche ou impressas em suas duas faces) elas poderão ser visualizadas independentemente através das laminas dos óculos polarizadores (neste caso são também chamados de analisadores). Partindo-se da constatação que no processo uma imagem não interfere na outra, a visualização através do par de óculos polarizados propicia uma fantástica observação em terceira dimensão direta em chapas transparentes de grandes dimensões.
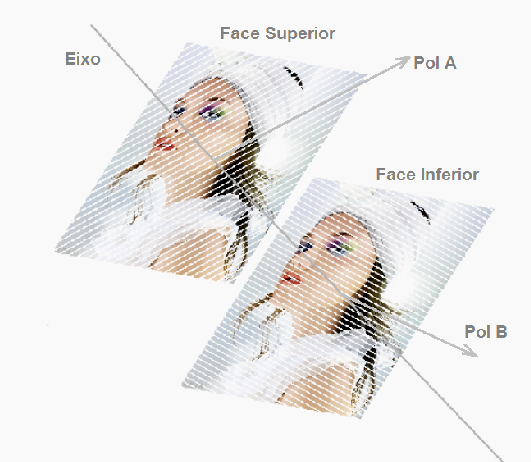
Fig. 27
Montagem de uma Vectografía polarizada
Outro interessantíssimo uso da polarização se encontra na projeção em 3D. O processo atingiu seu auge na década de 50 do século passado. O processo consistia em filmar uma cena com duas câmaras de cinema apropriadamente dispostas, que para simularem a visão humana, filmavam com as laterais invertidas. No processo de cópia esta falha era corrigida. Então dois projetores adequadamente dispostos e absolutamente sincronizados efetuavam a projeção simultânea sobre uma tela plana de alumínio. Cada projetor projetava sua imagem que atingia a tela com centro absoluto, através de um filtro polarizado a 45°. Um para a direita e o outro para a esquerda, formando assim ângulos de 90° entre si. O espectador usava um par de óculos de H-Polaroid com as duas respectivas angulações, assim o que via o olho direito não poderia ver o esquerdo, e vice versa. Estava formado o efeito tridimensional. A figura 28 demonstra o funcionamento desta engenhosidade.
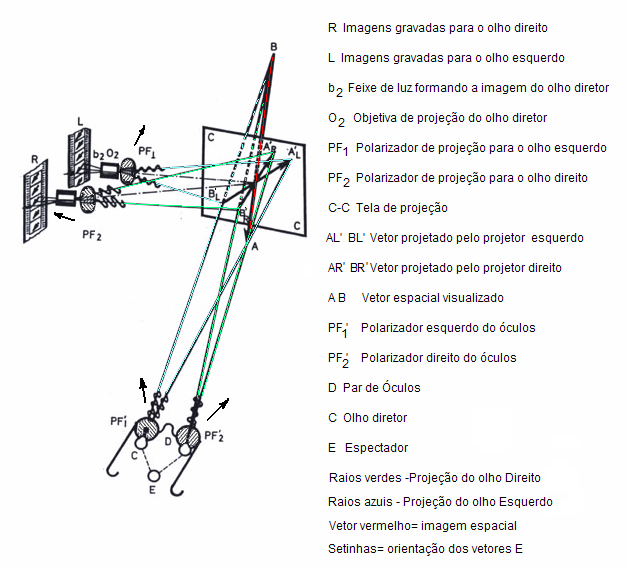
Fig. 28
Visualização da projeção em 3D através de filtros polarizadores
Ambos processos de imagem com polarização, apesar de estarem incluídos em usos da polarização, são também processos fotográficos históricos e lá estaremos em futuro desenvolvendo.
A Lei de Malus
A irradiância de uma luz polarizada plana que passa através de um polarizador é dada pela "Lei de Malus".
|
E = Eo cos2f |
Equação 2 |
|
onde: |
E |
= |
Irradiação transmitida através do filtro |
|
Eo |
= |
Máxima irradiação transmitida |
|
|
f |
= |
Ângulo entre o eixo de transmissão do polarizador e o plano de polarização da luz incidente. (Veja Figura 29.) |
Nota: Em muitas referências à Lei de Malus, a intensidade I é usada no lugar da irradiância E. Mantendo E como a irradiância, medidas em unidades de potência/área., A Equação 2 é dada em termos de E.
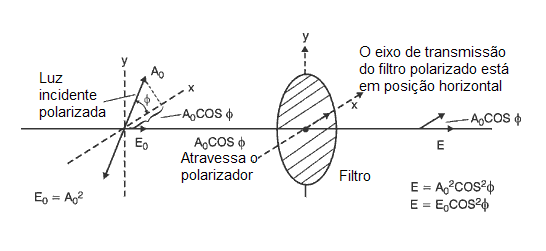
Fig. 29
Lei de Malus
Observe na figura 29, que o vetor de campo elétrico linearmente polarizado incidente de amplitude Ao, está vibrando em um ângulo f em relação ao eixo dos x. O componente de Ao ao longo dos eixo dos x é Ao cos f. É somente este componente que passa através do filtro polarizador, cujo eixo de transmissão é horizontal, Isto é, paralelo ao eido dos x. A partir de que a irradiação é igual ao quadrado da amplitude, a luz de incidente tem a irradiação Eo igual a Ao2, e a luz emergente tem a irradiância E igual a Ao2 cos2 f, ou E = Eo cos2 f, esta é a lei de Malus.
Por exemplo, se a transmissão máxima de um filtro de polarização é 90% e seu eixo de transmissão horizontal é orientado em 30° ao plano de incidência da luz polarizada, então, usando-se a equação 2,
E = 0.90 Eo cos2 30° = 0.675 Eo
Desde que T = E/Eo = 0.675, a transmissão do filtro é de 67.5%.
Observe que, se a área do feixe é inalterada enquanto passa através do filtro, a equação 2 poderá ser escrita como:
|
P = Po cos2 f |
Equação 3 |
onde P e Po são dados em unidades de potência e não em irradiância.
Além disso, você pode computar a transmissão de uma série de polarizadores lineares pela aplicação sucessiva da lei de Malus. Combinações mais complexas de filtros de polarização (placas de um quarto de onda, placas de meia onda, e assim por diante) podem ser facilmente avaliadas pela teoria vetorial de Jones, uma técnica poderosa de matrizes explicada em vários textos de óptica.
Célula de Kerr / Câmaras Rapatronic

Fig. 30
Explosão Nuclear. Línguas de fogo pelas aberturas do invólucro da bomba
Durante o início dos experimentos com a bomba atômica lá pelos anos 40, os cientistas nucleares tiveram alguma dificuldade em estudarem o crescimento da bola de fogo nos testes de detonações nucleares. Estas bolas de fogo expandiam tão rapidamente que mesmo as melhores câmeras daquela época eram incapazes de capturar qualquer coisa mais do que um quadro obscuro, superexposto quando a explosão se realizava.
Mas um professor da engenharia elétrica do MIT, o Dr. Harold Eugene Edgerton já havia inventado a câmera rapatronic, um dispositivo capaz de capturar imagens em extrema rapidez tal como no breve instante que segue diretamente uma explosão nuclear. Estas câmeras de único uso podiam registrar uma foto a um décimo milésimo de segundo após a detonação da bomba a uma distância aproximada de sete milhas, com uma duração de exposição de apenas dez nanosegundos. Nesse momento, uma bola de fogo nuclear típica já havia tinha alcançado aproximadamente 30 metros de diâmetro, com temperaturas da ordem de três vezes a da superfície do sol.
Edgerton foi um pioneiro na fotografia de alta velocidade, recebendo uma medalha de bronze da Royal Photographic Society em 1934 para seu trabalho do estroboscópio na fotografia. Usou a técnica para fotografar muitos eventos em que as câmeras típicas eram demasiado lentas capturar, como o instante de um balão que estoura, e os instantes em que as balas impactam vários materiais. Desenvolveu a câmera rapatronic aproximadamente dez anos mais tarde, com a finalidade específica de fotografar explosões nucleares para o governo.

Fig. 31
Câmara Rapatronic do Dr. Edgerton.
Em uma instalação típica no local da prova nuclear, uma série de dez ou mais câmeras rapatronic eram necessárias, porque cada uma podia tomar somente uma fotografia… pois nenhum sistema mecânico de avanço de película seria eficientemente rápido o bastante para permitir uma segunda foto. Uma outra limitação mecânica que tinha que ser superada era o mecanismo do obturador. Os obturadores mecânicos eram incapazes de mover-se bastante rápido para capturar a imagem em um décimo milionésimo de um segundo após a detonação, assim, o Dr. Edgerton desenvolveu as engenhosas câmeras que usavam um obturador original não mecânico que utilizava a polarização da luz.
Como você já percebeu, se você toma duas unidades de vidro polarizado (tais como as lentes de óculos de sol polarizados) e os coloca um sobre o outro em ângulos de 90°, nenhuma luz poderá passar. Pois cada uma filtra a luz que não é polarizada para seu eixo de polarização, e as duas unidades de polarização assim dispostas filtram 100% de toda a luz. Edgerton em sua câmera rapatronic usou esta propriedade em combinada com uma célula de Kerr - um elemento ótico muito engenhoso e ao mesmo tempo desconhecido que gira o plano de polarização quando um campo elétrico de alta tensão lhe é aplicado.

Fig. 32
Explosão nuclear. Efeito dos cabos de sustentação
A lente de câmera rapatronic inclui dois polarizadores perpendiculares, que impedem toda a entrada de luz … mas entre eles, montado como um “sandwich” está uma célula de Kerr. Quando a célula de Kerr é energizada, ela afeta a luz que passou através do primeiro polarizador girando seu plano de polarização em 90°, realinhando a onda de luz que assim combina com o segundo polarizador. Permitindo assim que a luz passe através de ambos os polarizadores sempre que a célula de Kerr for excitada pelo campo elétrico, que é exatamente o que se realiza durante 10 nanossegundos no momento crítico. Este conjunto cria um obturador não mecânico extremamente rápido, expondo a película à luz em uma minúscula fração de tempo.
Fotografias extraordinárias resultantes desta combinação revelaram detalhes intricados do primeiro instante de uma explosão atômica, incluindo algumas surpresas tais como o movimento irregular causado primeiramente por variações na densidade e conformação da bomba propriamente dita. Igualmente mostrou os detalhes do "efeito truque da corda", onde a vaporização rápida dos cabos de sustentação formavam linhas curiosas emanadas pela parte inferior da explosão. Mas mesmo excluindo-se da utilidade científica das imagens, certamente estas imagens mostram que estas bolas de fogo nucleares fantasticamente destrutivas têm seu lado tenebrosamente bonito, mesmo que somente por um décimo milésimo de um segundo.
O efeito optico-eléctrico de Kerr, ou o efeito DC. Kerr, é um caso especial em que o campo elétrico é um campo externo de variação aplicado, por exemplo, por uma tensão nos eletrodos dispostos no material a sofrer a alteração. Sob a influência do campo aplicado, o material torna-se birefringente, com índices de refração à luz diferentes polarizando-se paralela ou a perpendicularmente ao campo aplicado. A diferença no índice de refração, Δn, é dada pela fórmula:
![]()
onde o λ é o comprimento de onda da luz, K é a constante de Kerr, e E é a amplitude do campo elétrico. Esta diferença no índice de refração faz com que o material atue como uma barreira de onda quando a luz é incidente nele perpendicularmente ao sentido do campo elétrico. Se o material é colocado entre dois; polarizadores lineares cruzados (perpendiculares entre si), nenhuma luz será transmitida enquanto o campo elétrico estiver desligado, mas quase toda a luz será transmitida quando um valor adequado de campo elétrico for nele aplicado. Valores mais elevados da constante de Kerr permitem que a transmissão completa seja conseguida com um campo elétrico aplicado menor.
Alguns líquidos polares, tais como o nitrotolueno (C7H7NO2) e o nitrobenzene (C6H5NO2) exibem constantes de Kerr muito grandes. Uma célula de vidro enchida com um destes líquidos é chamada de Célula de Kerr. Estes elementos são usados freqüentemente para modular a luz, uma vez que o efeito de Kerr responde muito rapidamente às mudanças no campo elétrico. A luz pode ser modulada com estes dispositivos em freqüências tão elevadas quanto 10 Gigahertz. O fato do efeito de Kerr ser relativamente fraco faz com que uma célula de Kerr típica exija tensões elevadas da ordem de 30 quilovolts para que se consiga a transparência completa. Isto ocorre em contraste com as Células de Pockels, que podem se operar em tensões muito mais baixas. Uma outra desvantagem das células de Kerr é que o melhor material disponível, o nitrobenzeno, é venenoso. Alguns cristais transparentes foram usados igualmente para a modulação de Kerr, embora tivessem constantes menores de Kerr.
Diagramas de utilização da célula de Kerr e utilização nas câmaras rapatronic.
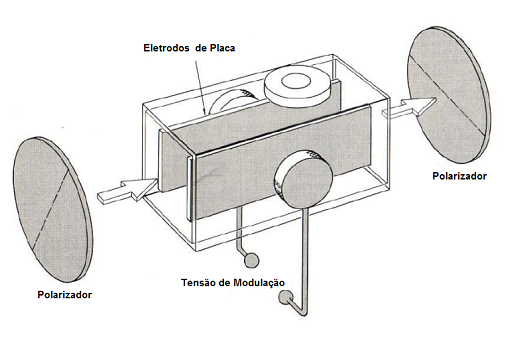
Fig. 33
Primeiro tipo de célula de Kerr
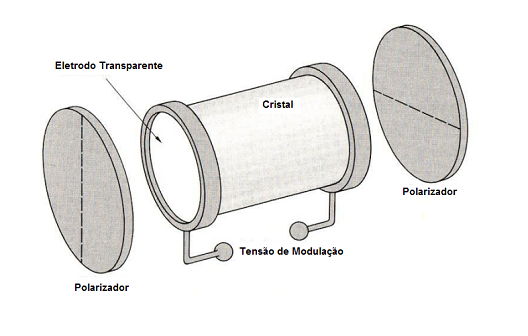
Fig. 34
Segundo tipo de célula de Kerr
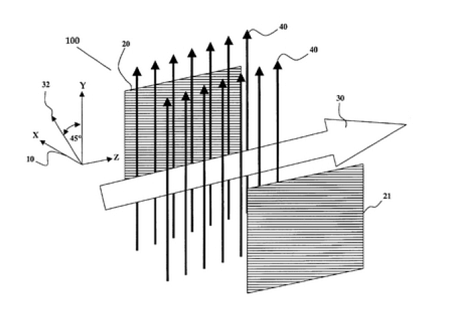
Fig.
35
Campos elétricos que ocorrem na de célula de Kerr
100=raio incidente, 20 e 21=filtros polarizadores, 30=Vetor M, 40=Vetores E, 10=triedro xyz, 32=rotação de E
Referencias
Austin, Russell. "Thin Film Polarizing Devices," Electro-Optical Svstems Design. Feb. 1974.
Jacobs, Donald. Fundamentals of Optical Engineering. McGraw Hill Book Co., 1943.
Jenkins, Francis A., and Harvey E. White. Fundamentals of Optics, 4th Edition. New York: McGraw-Hill Book Company, 1976.
Pedrotti, Frank L., and Leno S. Pedrotti. Introduction to Optics. Englewood Cliffs, NJ: Prentice-Hall, Inc., 1987.
University of Leicester
Herb Yeates' page on Rapatronic photographs
Wikipedia article on Herald Edgerton
Wikipedia article on the Rope Trick Effect
Diagram of a Kerr cell
Damn Interesting article 23 March 2006.
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX